题目内容
1.张老师带学生暑假去某地旅游考察,向导要求大家上山时多带一件衣服,并在介绍当地山区地理环境时说,海拔每增加100米,气温下降0.6℃,张老师在山脚下看了一下随身带的温度计,气温为30℃,试写出山上气温T(℃)与该处距山脚垂直高度h(m)之间的函数关系式,当张老师到达山顶时,发现温度为8℃,求山高.分析 (1)海拔每上升100米,温度下降0.6度,所以可得h=$\frac{30-T}{0.6}$×100,利用待定系数法求解;
(2)代入气温就可求出函数值即海拔高度h的值.
解答 解:(1)根据题意有h=$\frac{30-T}{0.6}$×100,
6h=30000-1000T,
T=30-0.006h;
(2)依题意有
8=30-0.006h,
解得h=3666$\frac{2}{3}$.
故山高3666$\frac{2}{3}$米.
点评 本题主要考查函数关系式,关键是待定系数法求出函数解析式.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
9.如果$\frac{3x}{{x}^{2}-3x}$=$\frac{3}{x-3}$,则x应满足的条件是( )
| A. | x≠0 且x≠3 | B. | x≠0或x≠3 | C. | x>0 | D. | x≠0 |
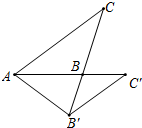 如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.
如图,△ABC中,∠ABC>90°,tan∠BAC=$\frac{3}{4}$,BC=4,将三角形绕着点A旋转,点C落在直线AB上的点C′处,点B落在点B′处.若C、B、B′恰好在一直线上,则AB的长为$\frac{6\sqrt{10}}{5}$.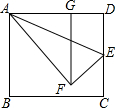 在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$.
在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$.
 如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.
如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.