题目内容
4. 已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:
已知三角形A′B′C′是由三角形ABC经过平移得到的,它们各顶点在平面直角坐标系中的坐标如下表所示:| 三角形ABC | A(a,2) | B(-5,1) | C(-2,0) |
| 三角形A′B′C′ | A′(3,4) | B′(1,b) | C′(c,2) |
(2)画出三角形ABC和三角形A′B′C′.
分析 (1)根据点A、A'、B、B'的坐标可得,三角形A'B'C'是三角形ABC先向右平移6个单位,然后向上平移两个单位,得出的图形,据此求出a、b、c的值;
(2)根据坐标作出两个三角形.
解答 解:∵A(a,2),A′(3,4),B(-5,1),B′(1,b),
∴三角形A'B'C'是三角形ABC先向右平移6个单位,然后向上平移两个单位得出的图形,
则a=-3,b=3,c=4;
(2)所作图形如图所示:
故答案为:-3,3,4.
点评 本题考查了根据平移变换作图,解答本题的关键是根据所给点的坐标判断出三角形A'B'C'是三角形ABC先向右平移6个单位,然后向上平移两个单位得出的图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.如果$\frac{3x}{{x}^{2}-3x}$=$\frac{3}{x-3}$,则x应满足的条件是( )
| A. | x≠0 且x≠3 | B. | x≠0或x≠3 | C. | x>0 | D. | x≠0 |
14.已知甲、乙两个班级各有50名学生.为了了解甲、乙两个班级学生解答选择题的能力状况,黄老师对某次考试中8道选择题的答题情况进行统计分析,得到统计表如下:
请根据以上信息解答下列问题:
(1)甲班学生答对的题数的众数是6;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=30%(优秀率=$\frac{班级优秀人数}{班级总人数}$×100%).
(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,画出树状图或列表求出抽到的2人在同一个班级的概率.
| 人数(人) 答对的题数(道) 班级 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 甲班 | 0 | 1 | 1 | 3 | 4 | 11 | 16 | 12 | 2 |
| 乙班 | 0 | 1 | 0 | 2 | 5 | 12 | 15 | 13 | 2 |
(1)甲班学生答对的题数的众数是6;
(2)若答对的题数大于或等于7道的为优秀,则乙班该次考试中选择题答题的优秀率=30%(优秀率=$\frac{班级优秀人数}{班级总人数}$×100%).
(3)从甲、乙两班答题全对的学生中,随机抽取2人作选择题解题方法交流,画出树状图或列表求出抽到的2人在同一个班级的概率.
 如图,写一个使AB∥CD的条件∠D=∠MAB或∠D+∠DAB=180°或∠B=∠DCN或∠B+∠DCB=180°.
如图,写一个使AB∥CD的条件∠D=∠MAB或∠D+∠DAB=180°或∠B=∠DCN或∠B+∠DCB=180°.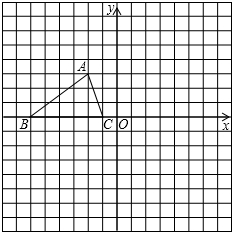 如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).
如图,已知△ABC的三个顶点的坐标分别为A(-2,3)B(-6,0),C(-1,0).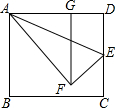 在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$.
在矩形ABCD中,AD=15,点E在边DC上,联结AE,△ADE沿直线AE翻折后点D落到点F,过点F作FG⊥AD,垂足为点G,如图,如果AD=3GD,那么DE=3$\sqrt{5}$. AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,且KG2=KD•KE.
AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K,且KG2=KD•KE. 如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.
如图,已知AB∥EF,AC、CE交于点C,求∠BAC+∠ACE+∠CEF的度数.