题目内容
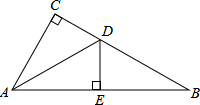 如图,在△ABC中,∠C=90°,AC=
如图,在△ABC中,∠C=90°,AC=| 1 |
| 2 |
考点:含30度角的直角三角形
专题:
分析:先在直角△ABC中,利用正弦函数的定义得出sinB=
=
,根据特殊角的三角函数值得到∠B=30°,由直角三角形两锐角互余求出∠BAC=60°.
| AC |
| AB |
| 1 |
| 2 |
解答:解:∵在△ABC中,∠C=90°,AC=
AB,
∴sinB=
=
,
∴∠B=30°,
∴∠BAC=90°-∠B=60°,
∴∠B<∠BAC.
| 1 |
| 2 |
∴sinB=
| AC |
| AB |
| 1 |
| 2 |
∴∠B=30°,
∴∠BAC=90°-∠B=60°,
∴∠B<∠BAC.
点评:本题考查了解直角三角形,三角函数的定义,特殊角的三角函数值,三角形内角和定理,比较简单.求出∠B=30°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在如下的一些数中:-3,3.14,-20,6.8,-
,|-9|,-32中是负整数的个数为( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
下列代数式中,不是单项式的是( )
A、
| ||
B、-
| ||
| C、t | ||
| D、3a2b |
 如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.
如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.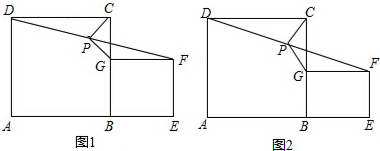
 如图,在△ABC中,∠C=90°,AD平分∠BAC,若AB=10,BD=4,则tan
如图,在△ABC中,∠C=90°,AD平分∠BAC,若AB=10,BD=4,则tan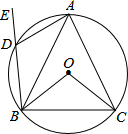 如图所示,⊙O是△ABC的外接圆,D是
如图所示,⊙O是△ABC的外接圆,D是