题目内容
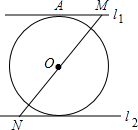 如图所示,直线l1∥l2,点M、N分别为l1、l2上的点,点O为MN的中点,以点O为圆心作⊙O与l1相切,切点为A.求证:⊙O与L2相切.
如图所示,直线l1∥l2,点M、N分别为l1、l2上的点,点O为MN的中点,以点O为圆心作⊙O与l1相切,切点为A.求证:⊙O与L2相切.考点:切线的判定与性质
专题:证明题
分析:如图,作辅助线,首先证明OB⊥l2;然后证明OB=OA,问题即可解决.
解答: 解:如图,连接AO并延长,交l2于点B;
解:如图,连接AO并延长,交l2于点B;
∵l1切⊙O于点A,
∴OA⊥AM;
又∵直线l1∥l2,
∴AB⊥l2,即OB⊥l2;△OAM∽△OBN,
∴
=
,
∵OM=ON,
∴OB=OA,
即圆心O到直线l2的距离等于⊙O的半径,
∴⊙O与L2相切.
 解:如图,连接AO并延长,交l2于点B;
解:如图,连接AO并延长,交l2于点B; ∵l1切⊙O于点A,
∴OA⊥AM;
又∵直线l1∥l2,
∴AB⊥l2,即OB⊥l2;△OAM∽△OBN,
∴
| OA |
| OB |
| OM |
| ON |
∵OM=ON,
∴OB=OA,
即圆心O到直线l2的距离等于⊙O的半径,
∴⊙O与L2相切.
点评:该命题主要考查了圆的切线的判定及其性质的应用问题;解题的关键是作辅助线,运用:圆心到直线的距离等于半径的直线为圆的切线这一判定方法,来完成解答.

练习册系列答案
相关题目
在如下的一些数中:-3,3.14,-20,6.8,-
,|-9|,-32中是负整数的个数为( )
| 1 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于
如图,在等腰梯形ABCD中,AD∥BC,AB=3,∠B=60°,DE∥AB,则CE等于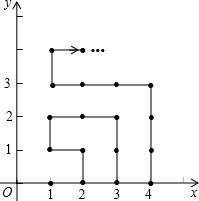 如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为
如图,在平面直角坐标系中,有若干个横、纵坐标分别为整数的点,其顺序按图中点的坐标分别为(1,0),(2,0),(2,1),(1,1),(1,2),(2,2),…的规律排列,根据这个规律,第2015个点的横坐标为 “健康、快乐、向上”立方体纸盒表面展开图如图,则与印有“健”字面相对的表面上印有
“健康、快乐、向上”立方体纸盒表面展开图如图,则与印有“健”字面相对的表面上印有 如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.
如图所示,⊙O的半径为R,弦AB,CD相互垂直,连接AD,BC.