题目内容
2.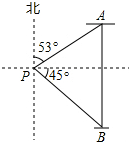 如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)
如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)【参考数据:sin53°=0.799,cos53°=0.602,tan53°=1.327】
分析 通过解直角△ACP得到AC、PC的长度;然后结合等腰直角三角形的性质来求BC的长度,则易求AB=AC+BC.
解答 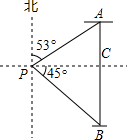 解:由题意,得∠A=53°,BC=PC.
解:由题意,得∠A=53°,BC=PC.
在直角△APC中,AC=100cos53°=100×0.602=60.2,
BC=PC=100sin53°=100×0.799=79.9,
所以AB=AC+BC=60.2+79.9=140.1≈140(海里).
答:两艘轮船之间的距离AB约为140海里.
点评 此题考查了解直角三角形的应用,此题是一道方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
10. 如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )
如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )
 如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )
如图,AB∥CD,点E在直线CD上,EA平分∠CEB,若∠BED=40°,则∠A大小为( )| A. | 80° | B. | 70° | C. | 50° | D. | 40° |
7. 某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:
某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:
根据上面提供的信息回答下列问题:
(1)统计表中m的值为11,并补全频数分布直方图;
(2)预习时间的中位数落在第3组;
(3)估计该校初一年级400名学生中,数学学科预习时间少于10分钟的学生人数.
 某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:
某中学为了了解初一年级学生数学学科的预习时间,在初一年级随机抽取了若干名学生进行调查,并把调查结果绘制成如下的不完整的统计表和统计图:| 组别 | 预习时间x(分钟) | 频数 |
| 1 | 0≤x<5 | 8 |
| 2 | 5≤x<10 | m |
| 3 | 10≤x<15 | 18 |
| 4 | 15≤x<20 | 13 |
| 合计 | 50 |
(1)统计表中m的值为11,并补全频数分布直方图;
(2)预习时间的中位数落在第3组;
(3)估计该校初一年级400名学生中,数学学科预习时间少于10分钟的学生人数.
11.化简$({-\frac{b}{a}})÷\frac{b}{{{a^2}-a}}$的结果是( )
| A. | -ab+1 | B. | -ab+b | C. | -a+1 | D. | -a-1 |
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为2.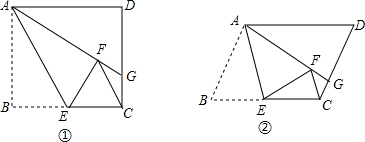

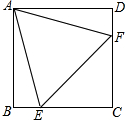 如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.
如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.