题目内容
12.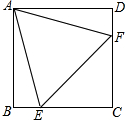 如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.
如图,正方形ABCD中,E、F分别是BC,CD边上的点,且△AEF是等边三角形,若BE=1cm,则正方形ABCD的边长是2+$\sqrt{3}$cm.
分析 在AB上取一点M使得AM=ME,先证明△ABE≌△ADF得∠BAE=∠DAF=15°,再在RT△BME中求出EM、EB即可解决问题.
解答 解:如图,在AB上取一点M使得AM=ME,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
∵△AEF是等边三角形,
∴AE=AF,∠EAF=60°,
在RT△ABE和RT△ADF中,
$\left\{\begin{array}{l}{AB=AD}\\{AE=AF}\end{array}\right.$,
∴△ABE≌△ADF,
∴∠BAE=∠DAF=15°,
∵AM=ME,
∴∠MAE=∠MEA=15°,
∴∠EMB=30°,
在RT△EMB中,∵∠B=90°,BE=1,∠EMB=30°,
∴AM=ME=2BE=2,BM=$\sqrt{3}$,
∴AB=AM+BM=2+$\sqrt{3}$.
故答案为2+$\sqrt{3}$.
点评 本题考查正方形的性质、等边三角形的性质、勾股定理等知识,解题的关键是添加辅助线构造30度的直角三角形,学会出现15度角想到这个添加辅助线方法,属于中考常考题型.

练习册系列答案
相关题目
7.连掷两枚质地均匀的骰子,它们的点数相同的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{6}$ |
4.如果把分式$\frac{2n}{m-n}$中的m和n都扩大2倍,那么分式的值( )
| A. | 不变 | B. | 扩大2倍 | C. | 缩小2倍 | D. | 扩大4倍 |
2. 为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
(1)表中m=0.2;n=80;本次比赛成绩的中位数落在分数段70≤x<80中;
(2)补全条形统计图;
(3)如果比赛成绩80分以上(含80分)为优秀,全校参加比赛的800名同学中,优秀人数大约有多少人?
 为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:
为了解中学生对我国汉子的掌握情况,某校组织了“汉字知识大赛”活动,随机调查了部分参赛同学的成绩,整理并制作图表如下:| 分 数 段 | 频数 | 频率 |
| 90≤x<100 | 20 | 0.1 |
| 80≤x<90 | 40 | m |
| 70≤x<80 | n | 0.4 |
| 60≤x<70 | 60 | 0.3 |
(2)补全条形统计图;
(3)如果比赛成绩80分以上(含80分)为优秀,全校参加比赛的800名同学中,优秀人数大约有多少人?
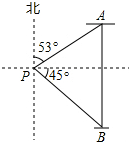 如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)
如图,一艘货轮位于灯塔P北偏东53°方向,距离灯塔100海里的A处,另一艘客轮位于货轮正南方向,且在灯塔P南偏东45°方向的B处,求此时两艘轮船之间的距离AB.(结果精确到1海里)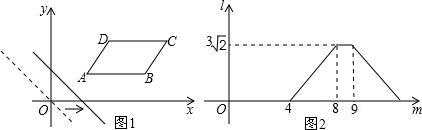
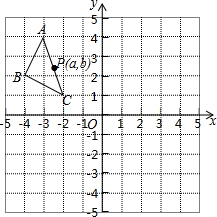 如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.
如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(-3,4),B(-4,2),C(-2,1),△ABC绕原点逆时针旋转90°,得到△A1B1C1,将△A1B1C1向右平移6个单位,再向上平移2个单位得到△A2B2C2.