题目内容
3.已知a+b2+|$\sqrt{c-1}$-1|=4$\sqrt{a-2}$+2b-3,求a+2b-$\frac{1}{2}$c的值.分析 首先移项,利用完全平方公式分组分解因式,进一步利用非负数的性质得出a、b、c的数值,进一步代入得出答案即可.
解答 解:∵a+b2+|$\sqrt{c-1}$-1|=4$\sqrt{a-2}$+2b-3,
∴a-2-4$\sqrt{a-2}$+4+b2-2b+1+|$\sqrt{c-1}$-1|=0,
即($\sqrt{a-2}$-2)2+(b-1)2+|$\sqrt{c-1}$-1|=0,
∴$\sqrt{a-2}$-2=0,b-1=0,$\sqrt{c-1}$-1=0,
∴a=6,b=1,c=2,
∴a+2b-$\frac{1}{2}$c=6+2-1=7.
点评 此题考查配方法的运用,非负数的性质,利用完全平方公式因式分解,掌握二次根式的性质是解决问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 a、b、c三个数在数轴上的对应位置如图所示,化简:|a|-|a+b|+|c-b|+|a+c|.
a、b、c三个数在数轴上的对应位置如图所示,化简:|a|-|a+b|+|c-b|+|a+c|. 如图,EF⊥AD.垂足为G,DE=AE,DE∥AC,求证:∠FAC=∠B.
如图,EF⊥AD.垂足为G,DE=AE,DE∥AC,求证:∠FAC=∠B.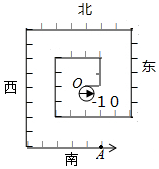 把一数轴折成如图所示,第1段为1个单位长度,第2段为2个单位长度,第3段为3个单位长度,…点O处有一个圆,圆上刻一指针,开始指针朝东,圆周为4个单位长度,圆紧贴数轴沿着数轴的正方向滚动,当圆与点A接触时,指针指向北(东、南、西、北),当圆与2015接触时,指针指向北(东、南、西、北).
把一数轴折成如图所示,第1段为1个单位长度,第2段为2个单位长度,第3段为3个单位长度,…点O处有一个圆,圆上刻一指针,开始指针朝东,圆周为4个单位长度,圆紧贴数轴沿着数轴的正方向滚动,当圆与点A接触时,指针指向北(东、南、西、北),当圆与2015接触时,指针指向北(东、南、西、北).