题目内容
13.计算:$\frac{({2}^{2}+{4}^{2}+…+10{0}^{2})-({1}^{2}+{3}^{2}+…+9{9}^{2})}{1+2+3+…+10+9+…+2+1}$.分析 首先把分子分组,两个连续自然数的平方组合,利用平方差公式因式分解后计算,分母利用凑10的方法计算出结果,再把分子分母约分得出答案即可.
解答 解:原式=$\frac{({2}^{2}-{1}^{2})+({4}^{2}-{3}^{2})+…+(10{0}^{2}-9{9}^{2})}{10+10+10+…+10}$
=$\frac{3+7+11+…+199}{100}$
=$\frac{1+2+3+4+5+6+…+99+100}{100}$
=$\frac{\frac{1}{2}×100×(100+1)}{100}$
=50.5.
点评 此题考查因式分解的实际运用,掌握平方差公式是解决问题的关键.

练习册系列答案
相关题目
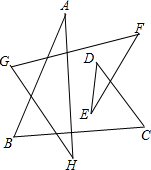 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°.
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=360°. 在如图所示网格内建立恰当直角坐标系后,画出函数y=2x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1).
在如图所示网格内建立恰当直角坐标系后,画出函数y=2x2和y=-$\frac{1}{2}$x2的图象,并根据图象回答下列问题(设小方格的边长为1).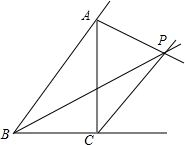 如图,已知△ABC的两外角平分线AP,CP相交于点P,连接BP,若∠BPC=40°,求∠CAP的度数.
如图,已知△ABC的两外角平分线AP,CP相交于点P,连接BP,若∠BPC=40°,求∠CAP的度数.