题目内容
14.已知△ABC中,a2+b2+c2=10a+24b+26c-338,则c=13,△ABC的形状是直角三角形.分析 将a2+b2+c2=10a+24b+26c-338进行配方,求出a,b,c,根据勾股定理的逆定理判断△ABC的形状.
解答 解:∵a2+b2+c2=10a+24b+26c-338,
∴a2-10a+25+b2-24b+144+c2-26c+169=0,
∴(a-5)2+(b-12)2+(c-13)2=0,
∴a-5=0,b-12=0,c-13=0,即a=5,b=12,c=13.
∵52+122=132,
∴△ABC是直角三角形.
故答案为:13,直角三角形.
点评 此题考查因式分解的运用,非负数的性质,以及勾股定理逆定理的运用,利用完全平方公式分解因式是解决问题的前提.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
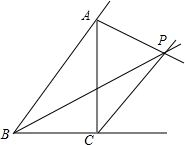 如图,已知△ABC的两外角平分线AP,CP相交于点P,连接BP,若∠BPC=40°,求∠CAP的度数.
如图,已知△ABC的两外角平分线AP,CP相交于点P,连接BP,若∠BPC=40°,求∠CAP的度数.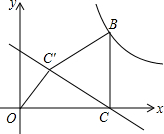 点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).
点C在x的正半轴上,且BC⊥OC于点C,将线段BC绕点B顺时针旋转60°至BC′位置,且点C′的坐标为(2,2$\sqrt{3}$).