题目内容
有一种活鱼,在室内暂养最多只能存活两天,如果放养在塘内,可以延长存活时间,但每天也有一定的数量死去.假设放养期内鱼的个体重量保持不变.小王,按市场价50元/千克收购了这种活鱼1吨放养租用30天塘内.据市场变化,此后每天每千克活鱼价格可上升2元,但是,放养一天需各种费用支出400元,且平均每天还有10千克的鱼死去,假定死鱼均于当天全部售出,售价都是每千克30元.
(1)如果放养x天后将活鱼一次性出售,并记1吨鱼的销售总额为W元,写出W与x的函数关系式;
(2)该经销商将这批鱼放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用)?最大利润是多少?
(1)如果放养x天后将活鱼一次性出售,并记1吨鱼的销售总额为W元,写出W与x的函数关系式;
(2)该经销商将这批鱼放养多少天后出售,可获最大利润(利润=销售总额-收购成本-费用)?最大利润是多少?
考点:二次函数的应用
专题:
分析:(1)根据题意分别得出活鱼的销售额以及死鱼的销售额进而得出销售总额;
(2)设总利润为Q,则Q=W-50×1000-400x进而求出其最值.
(2)设总利润为Q,则Q=W-50×1000-400x进而求出其最值.
解答:解(1)由题意知:活鱼的销售额为:(1000-10x)(50+2x)元,
死鱼的销售额为:30×10x=300x元.
故W=(1000-10x)(50+x)+300x=-20x2+1800x+50000;
(2)设总利润为Q,则:
Q=W-50×1000-400x
=-20x2+1400x
=-20(x2-70x)
=-20(x-35)2+24500.
∵a=-20<0,∴当x<35时,Q随x的增大而增大.
当x=30时,总利润最大,最大利润为24000元.
死鱼的销售额为:30×10x=300x元.
故W=(1000-10x)(50+x)+300x=-20x2+1800x+50000;
(2)设总利润为Q,则:
Q=W-50×1000-400x
=-20x2+1400x
=-20(x2-70x)
=-20(x-35)2+24500.
∵a=-20<0,∴当x<35时,Q随x的增大而增大.
当x=30时,总利润最大,最大利润为24000元.
点评:此题主要考查了二次函数的应用以及二次函数最值求法,得出Q与x的函数关系式是解题关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
 如图,已知在△ABC中,AD是∠BAC的角平分线,AE是BC边上的高,且∠B=25°,∠C=55°,则∠DAE的度数是( )
如图,已知在△ABC中,AD是∠BAC的角平分线,AE是BC边上的高,且∠B=25°,∠C=55°,则∠DAE的度数是( )| A、15° | B、35° |
| C、65° | D、75° |
计算(5m2+15m3n-20m4)÷(-5m2)结果正确的是( )
| A、1-3mn+4m2 |
| B、-1-3m+4m2 |
| C、4m2-3mn-1 |
| D、4m2-3mn |
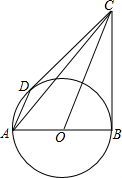 如图,AB是⊙O的直径,AB=6,D是⊙O上的动点(不同于A、B),过O作OC∥AD交过B点⊙O的切线于点C.
如图,AB是⊙O的直径,AB=6,D是⊙O上的动点(不同于A、B),过O作OC∥AD交过B点⊙O的切线于点C.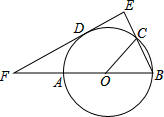 如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.
如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.