题目内容
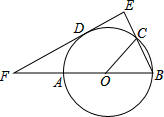 如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.
如图,C是直径为AB的圆O上一点,D是弧AC的中点,DE⊥BC于E,ED交BA的延长线于F.(1)求证:EF是圆0的切线;
(2)若DF=10
| 3 |
考点:切线的判定,弧长的计算
专题:
分析:(1)连接OD,求出∠E=∠ACB=∠ECA=∠DMC=90°,求出∠EDO=90°,证得OD⊥ME,从而判定切线;
(2)根据勾股定理求出半径,求出∠FOD,即可求出∠AOC,根据弧长公式求出弧AC的长即可.
(2)根据勾股定理求出半径,求出∠FOD,即可求出∠AOC,根据弧长公式求出弧AC的长即可.
解答:(1)证明:连接OD,AC,两线交于M,
∵点D是弧AC的中点,
∴OD⊥AC,
∵AB是直径,DE⊥BC,
∴∠E=∠ACB=∠ECA=∠DMC=90°,
∴∠EDO=360°-90°-90°-90°=90°,
∴OD⊥EF,
∵OD为半径,
∴EF是⊙O的切线;
(2)解:设OD=R,
则AF=OA=R,
在Rtβ△FDO中,FD2+DO2=FO2,
即(10
)2+R2=(2R)2,
解得:R=10,
即OD=R=10,OF=2R=20,
∴∠F=30°,∠FOD=60°,
∵D为弧AC的中点,
∴∠AOC=2×60°=120°,
∴弧AC的长是
=
π.

∵点D是弧AC的中点,
∴OD⊥AC,
∵AB是直径,DE⊥BC,
∴∠E=∠ACB=∠ECA=∠DMC=90°,
∴∠EDO=360°-90°-90°-90°=90°,
∴OD⊥EF,
∵OD为半径,
∴EF是⊙O的切线;
(2)解:设OD=R,
则AF=OA=R,
在Rtβ△FDO中,FD2+DO2=FO2,
即(10
| 3 |
解得:R=10,
即OD=R=10,OF=2R=20,
∴∠F=30°,∠FOD=60°,
∵D为弧AC的中点,
∴∠AOC=2×60°=120°,
∴弧AC的长是
| 120π×10 |
| 180 |
| 20 |
| 3 |
点评:本题考查了切线的判定,弧长公式,圆周角定理,勾股定理的应用,解题的关键是正确地作出辅助线,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若m<n,则下列不等式中,正确的是( )
| A、m-4>n-4 | ||||
B、
| ||||
| C、-3m<-3n | ||||
| D、2m+1<2n+1 |
若
=
,则q的值是( )
| 5 |
| q |
| 3 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
某餐厅共有7名员工,所有员工的工资如下所示:
则餐厅所有员工工资的众数,中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 服务员 |
| 人数 | 1 | 2 | 1 | 3 |
| 工资数 | 16000 | 6000 | 5200 | 3400 |
| A、3400,5200 |
| B、5200,3400 |
| C、340,5600 |
| D、5600,3400 |