Question

如图1，在⊙O中，直径AB⊥CD于点E，点P在BA的延长线上，且满足∠PDA=∠ADC．

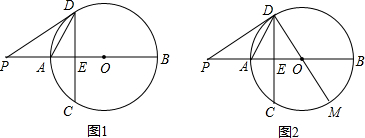
（1）判断直线PD与⊙O的位置关系，并说明理由；
（2）延长DO交⊙O于M（如图2），当M恰为

BC

的中点时，试求

DE

BE

的值；
（3）若PA=2，tan∠PDA=

1

2

，求⊙O的半径．

Answer 1

考点：圆的综合题

专题：

分析：（1）利用同弦所对的圆心角等于圆周角的2倍及直径AB⊥CD，得出∠PDO=90°，即可得出直线PD与⊙O相切，
（2）要求

DE

BE

的值；可连接BD，在RT△DBE中，只要求出∠DBA的度数即可，利用角的关系求出∠CDM=30°，即可得出∠DBA=30°，所以可求出

DE

BE

的值；
（3）可由tan∠PDA=

1

2

，求出DE与AE的关系，在RT△DEO中和RT△PDE中，运用勾股定理得出关系式，再结合切割线定理即可求出⊙O的半径为r．

解答：
解（1）直线PD与⊙O相切，
证明：如图1，连接DO，CO，
∵∠PDA=∠ADC．
∴∠PDC=2∠ADC
∵∠AOC=2∠ADC，
∴∠PDC=∠AOC，
∵直径AB⊥CD于点E，
∴∠AOD=∠AOC，
∴∠PDC=∠AOD，
∵∠AOD+∠ODE=90°，
∴∠PDC+∠ODE=90°，
∴直线PD与⊙O相切．

（2）如图2，连接BD，

∵M恰为

BC

的中点，
∴∠CDM=∠BDM，
∵∠BDM=∠DBA，
∴∠CDM=∠DBA，
∵直线PD与⊙O相切，
∴∠PDA=∠DBA，
∴∠PDA=∠CDM，
又∵∠PDA=∠ADC．
∴∠PDM=3∠CDM=90°，
∴∠CDM=30°，
∴∠DBA=30°，
∴

DE

BE

=tan30°=

3

3

．

（3）如图3，

∵tan∠PDA=

1

2

，∠PDA=∠ADC，
∴

AE

DE

=

1

2

，即DE=2AE，
在RT△DEO中，设⊙O的半径为r，DE²+EO²=DO²
∴（2AE）²+（r-AE）²=r²
解得r=

5

2

AE，
在RT△PDE中，DE²+PE²=PD²
∴（2AE）²+（2+AE）²=PD²
∵直线PD与⊙O相切，
∴PD²=PA•PB，即PD²=2×（2+2r）
∴（2AE）²+（2+AE）²=2×（2+2r）
化简得，5AE²+4AE=4r，
∵r=

5

2

AE，
解得，r=3．

点评：本题主要考查了圆的综合题，解题的关键是把切线性质与勾股定理相结合求线段．