题目内容
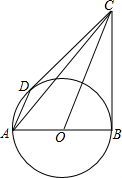 如图,AB是⊙O的直径,AB=6,D是⊙O上的动点(不同于A、B),过O作OC∥AD交过B点⊙O的切线于点C.
如图,AB是⊙O的直径,AB=6,D是⊙O上的动点(不同于A、B),过O作OC∥AD交过B点⊙O的切线于点C.(1)求证:CD与⊙O相切;
(2)设AD=x,OC=y,求y关于x的函数关系式;
(3)当AD=2时,求sin∠ACO的值.
考点:圆的综合题
专题:
分析:(1)先连接OD,得出∠1=∠3,∠2=∠DAO,根据∠3=∠DAO,得出∠1=∠2.从而证出△COD≌△COB,∠ODC=∠OBC,最后根据∠OBC=90°,得出∠ODC=90°,从而证出CD是⊙O的切线;
(2)连接DB,先证出∠ADB=90°,再根据∠COB=∠BAD,得出△ABD∽△OCB,证出
=
,即可得出答案;
(3)作OH⊥AC于H,求出OC=9,再根据BC=
,AC=
求出BC、AC,再根据△AOH∽△ACB,得出
=
,
=
,求出OH,从而求出sin∠ACO.
(2)连接DB,先证出∠ADB=90°,再根据∠COB=∠BAD,得出△ABD∽△OCB,证出
| x |
| 6 |
| 3 |
| y |
(3)作OH⊥AC于H,求出OC=9,再根据BC=
| OC2-OB2 |
| AB2-BC2 |
| OH |
| CB |
| AO |
| AC |
| OH | ||
6
|
| 3 | ||
6
|
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵OC∥AD,
∴∠1=∠3,∠2=∠DAO,
∵OA=OD,
∴∠3=∠DAO,
∴∠1=∠2.
在△COD和△COB中,
,
∴△COD≌△COB(SAS),
∴∠ODC=∠OBC.
∵CB切⊙O于B,
∴∠OBC=90°,
∴∠ODC=90°,OD⊥CD
∴CD是⊙O的切线.
(2)解:连接DB,
∵AB是直径,
∴∠ADB=90°.
∵∠COB=∠BAD,
∴△ABD∽△OCB,
∴
=
,
∴
=
,
∴y=
.
(3)解:作OH⊥AC于H,
由(2)得,OC=18÷2=9,
在△OCB中,
∵∠OBC=90°,
∴BC=
=
=6
.
在△ABC中,
∵∠ABC=90°,
∴AC=
=
=6
.
由△AOH∽△ACB,得
=
,
即
=
,
解得:OH=
,
则sin∠ACO=
=
.
 (1)证明:连接OD,
(1)证明:连接OD,∵OC∥AD,
∴∠1=∠3,∠2=∠DAO,
∵OA=OD,
∴∠3=∠DAO,
∴∠1=∠2.
在△COD和△COB中,
|
∴△COD≌△COB(SAS),
∴∠ODC=∠OBC.
∵CB切⊙O于B,
∴∠OBC=90°,
∴∠ODC=90°,OD⊥CD
∴CD是⊙O的切线.
(2)解:连接DB,
∵AB是直径,
∴∠ADB=90°.

∵∠COB=∠BAD,
∴△ABD∽△OCB,
∴
| AD |
| AB |
| OB |
| OC |
∴
| x |
| 6 |
| 3 |
| y |
∴y=
| 18 |
| x |
(3)解:作OH⊥AC于H,
由(2)得,OC=18÷2=9,

在△OCB中,
∵∠OBC=90°,
∴BC=
| OC2-OB2 |
| 92-32 |
| 2 |
在△ABC中,
∵∠ABC=90°,
∴AC=
| AB2-BC2 |
| 62+72 |
| 3 |
由△AOH∽△ACB,得
| OH |
| CB |
| AO |
| AC |
即
| OH | ||
6
|
| 3 | ||
6
|
解得:OH=
| 6 |
则sin∠ACO=
| OH |
| OC |
| ||
| 9 |
点评:此题考查圆的综合,用到的知识点是勾股定理、圆的有关性质、相似三角形和全等三角形的判定与性质、切线的判定,关键是作出辅助线构造直角三角形.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
计算(a4)2的结果是( )
| A、a8 |
| B、a6 |
| C、2a4 |
| D、a2 |
下列调查中,适宜采用全面调查方式的是( )
| A、调查春节联欢晚会在北京地区的收视率 |
| B、了解全班同学参加社会实践活动的情况 |
| C、调查某品牌食品的蛋白质含量 |
| D、了解一批手机电池的使用寿命 |
在平面直角坐标系中,点P(-1,4)在( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
某餐厅共有7名员工,所有员工的工资如下所示:
则餐厅所有员工工资的众数,中位数分别是( )
| 人员 | 经理 | 厨师 | 会计 | 服务员 |
| 人数 | 1 | 2 | 1 | 3 |
| 工资数 | 16000 | 6000 | 5200 | 3400 |
| A、3400,5200 |
| B、5200,3400 |
| C、340,5600 |
| D、5600,3400 |
 为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了一次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表:
为增强环境保护意识,争创“文明卫生城市”,某企业对职工进行了一次“生产和居住环境满意度”的调查,按年龄分组,得到下面的各组人数统计表: