题目内容
7.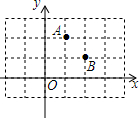 如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
分析 连接AB并延长交x轴于点M,作A点关于y轴的对称点A′连接A′B交y轴于点N,求出点N与y轴的交点坐标即可得出结论.
解答 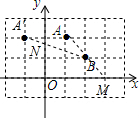 解:连接AB并延长交x轴于点M,由三角形的三边关系可知,点M即为x轴上使得|MA-MB|的值最大的点,
解:连接AB并延长交x轴于点M,由三角形的三边关系可知,点M即为x轴上使得|MA-MB|的值最大的点,
∵点B是2x2的正方形的对角线的交点,
∴点M即为AB延长线上的点,此时M(3,0)即OM=3;
作A点关于y轴的对称点A′连接A′B交y轴于点N,则A′B即为NA+NB的最小值,
∵A′(-1,2),B(2,1),
设过A′B的直线为:y=kx+b,则$\left\{\begin{array}{l}{2=-k+b}\\{1=2k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{3}}\\{b=\frac{5}{3}}\end{array}\right.$,
∴N(0,$\frac{5}{3}$),即ON=$\frac{5}{3}$,
∴OM•ON=3×$\frac{5}{3}$=5.
故答案为:5.
点评 本题考查的是轴对称-最短路线问题,根据题意得出M、N两点的坐标是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.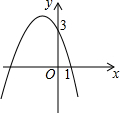 已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )
已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )
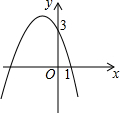 已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )
已知二次函数y=ax2+bx+c的图象如图所示,则函数关系式是( )| A. | y=x2-2x+3 | B. | y=-x2-2x+3 | C. | y=x2+2x+3 | D. | y=-x2+2x+3 |
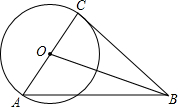 如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.
如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.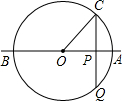 如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由.
如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由. 如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.
如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.