题目内容
17.计算:(1)$\frac{6a}{8b}•\frac{2{b}^{2}}{3a}$
(2)$\frac{{x}^{2}+x}{{x}^{2}}•\frac{x}{{x}^{2}-1}$
(3)$\frac{x}{{x}^{2}-3x}÷\frac{1}{{x}^{2}-9}$
(4)$\frac{{x}^{2}-2x+1}{{x}^{2}-1}÷\frac{x-1}{{x}^{2}+x}$.
分析 (1)根据分式的乘法,分子、分母约分,可得答案;
(2)根据分式的乘法,分子分母先分解因式,然后约分,可得答案;
(3)根据分式的除法,可得分式的乘法,根据分式的乘法,分子分母先分解因式,然后约分,可得答案;
(4)根据分式的除法,可得分式的乘法,根据分式的乘法,分子分母先分解因式,然后约分,可得答案.
解答 解:(1)原式=$\frac{b}{2}$;
(2)原式=$\frac{x(x+1)}{{x}^{2}}$•$\frac{x}{(x+1)(x-1)}$=$\frac{1}{x-1}$;
(3)原式=$\frac{x}{x(x-3)}$•(x+3)(x-3)=x+3;
(4)原式=$\frac{(x-1)^{2}}{(x+1)(x-1)}$•$\frac{x(x+1)}{x-1}$=x.
点评 本题考查了分式的乘除法,在完成此类化简题时,应先将分子、分母中能够分解因式的部分进行分解因式.有些需要先提取公因式,而有些则需要运用公式法进行分解因式.通过分解因式,把分子分母中能够分解因式的部分,分解成乘积的形式,然后找到其中的公因式约去.

练习册系列答案
相关题目
 日前一名男子报警称,在菲律宾南部发现印有马来西亚国旗的飞机残骸,怀疑是失联的马航MH370客机,马来西亚警方立即派出直升机前去查证.飞机在空中A点看见残骸C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见残骸C的俯角为45°,已知飞机的飞行度为3150米/分.
日前一名男子报警称,在菲律宾南部发现印有马来西亚国旗的飞机残骸,怀疑是失联的马航MH370客机,马来西亚警方立即派出直升机前去查证.飞机在空中A点看见残骸C的俯角为20°,继续沿直线AE飞行16秒到达B点,看见残骸C的俯角为45°,已知飞机的飞行度为3150米/分.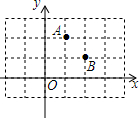 如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.