题目内容
15.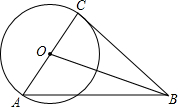 如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.
如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.
分析 解直角三角形求出BC,根据勾股定理求出OB,再根据直线与圆的位置关系得出即可.
解答 解:⊙B与⊙O的位置关系是外切,
理由是:∵在Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$,
∴$\frac{BC}{AC}$=$\frac{2}{3}$,
∴BC=8,
∵AC=12,
∴OC=6,
∴由勾股定理得:OB=$\sqrt{B{C}^{2}+O{C}^{2}}$=10,
∵⊙O的半径为6,⊙B的半径为4,
∴⊙B与⊙O的位置关系是外切.
点评 本题考查了解直角三角形,勾股定理,直线与圆的位置关系的应用,能求出OB的长是解此题的关键.

练习册系列答案
相关题目
20.将一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是( )
| A. | 圆柱的高 | B. | 圆柱的侧面积 | C. | 圆柱的体积 | D. | 圆柱的底面积 |
 如图,请用直尺和三角板根据要求作图:
如图,请用直尺和三角板根据要求作图: 如图,小明想用镜子测量一棵古松树AB的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,第一次他把镜子放在点C处,人在点F处正好看到树尖A;第二次他把镜子放在点C′处,人在点F′处正好看到树尖A,已知小明眼睛距地面1.6m,量得CC′=7m,CF=2m,C′F′=3m,求这棵古松树AB的高.
如图,小明想用镜子测量一棵古松树AB的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,第一次他把镜子放在点C处,人在点F处正好看到树尖A;第二次他把镜子放在点C′处,人在点F′处正好看到树尖A,已知小明眼睛距地面1.6m,量得CC′=7m,CF=2m,C′F′=3m,求这棵古松树AB的高.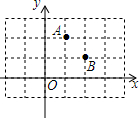 如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.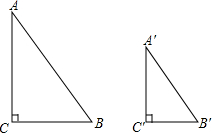 已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.