题目内容
12.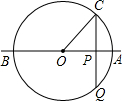 如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由.
如图,直线AB经过⊙O的圆心,且与⊙O相交于A,B两点,点C在⊙0上,且∠AOC是锐角.点P是直线AB上一个动点(不与点O重合),直线PC与⊙O相交于点Q,是否存在点P.使得QP=QO?如果存在,这样的点P共有几个?如果不存在,请说明理由.
分析 点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
解答 解:存在点P.使得QP=QO,这样的点P共有3个,
理由是:
①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图2),
∵OC=OQ,
∴∠OQP=(180°-∠QOC)×$\frac{1}{2}$①,
∵OQ=PQ,
∴∠OPQ=(180°-∠OQP)×$\frac{1}{2}$②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°-∠COQ)×$\frac{1}{2}$①,
∵OQ=PQ,
∴∠P=(180°-∠OQP)×$\frac{1}{2}$②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°-150°-10°=20°,
所以存在点P,使得QP=QO,这样的点P共有3个.
点评 本题主要考查了圆的认识及等腰三角形等边对等角的性质,先假设存在并进行分类讨论是进行解题的关键.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
20.将一个底面直径是10厘米,高为36厘米的圆柱体锻压成底面直径为20厘米的圆柱体,在这个过程中不改变的是( )
| A. | 圆柱的高 | B. | 圆柱的侧面积 | C. | 圆柱的体积 | D. | 圆柱的底面积 |
 如图,请用直尺和三角板根据要求作图:
如图,请用直尺和三角板根据要求作图: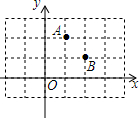 如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5. 如图所示,
如图所示,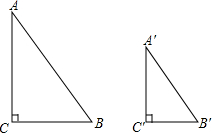 已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.