题目内容
16.解方程组:$\left\{\begin{array}{l}{\sqrt{3}x-\sqrt{2}y=\sqrt{2}}\\{x-\sqrt{6}y=1}\end{array}\right.$.分析 利用解方程组的方法与步骤求得x、y的数值,进一步化简即可.
解答 解:$\left\{\begin{array}{l}{\sqrt{3}x-\sqrt{2}y=\sqrt{2}①}\\{x-\sqrt{6}y=1②}\end{array}\right.$
由②得,x=1+$\sqrt{6}$y③
把③代入①得,$\sqrt{3}$(1+$\sqrt{6}$y)-$\sqrt{2}$y=$\sqrt{2}$,
解得:y=$\frac{2-\sqrt{6}}{4}$,
代入③得,x=$\frac{\sqrt{6}-1}{2}$,
所以原方程组的解为$\left\{\begin{array}{l}{x=\frac{\sqrt{6}-1}{2}}\\{y=\frac{2-\sqrt{6}}{4}}\end{array}\right.$.
点评 此题考查二次根式的运用,掌握解二元一次方程组的解法以及二次根式的化简是解决问题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
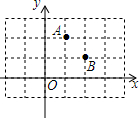 如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.
如图所示,点M是x轴上使得|MA-MB|的值最大的点,点N是y轴上使得NA+NB的值最小的点,则OM×ON=5.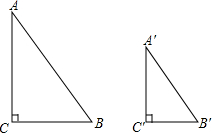 已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$.
已知:如图,在Rt△ABC和Rt△A′B′C′中,∠C=∠C′=90°,$\frac{AB}{A′B′}=\frac{AC}{A′C′}$. 如图所示,甲、乙两船同时从B地出发,甲船以每小时10(1+$\sqrt{3}$)海里的速度向正东方向航行.乙船以每小时20海里的速度沿着方位角120°的方向航行,1小时后甲、乙两船分别到达A、C两地.求A、C两地之间的距离(精确到0.1海里).
如图所示,甲、乙两船同时从B地出发,甲船以每小时10(1+$\sqrt{3}$)海里的速度向正东方向航行.乙船以每小时20海里的速度沿着方位角120°的方向航行,1小时后甲、乙两船分别到达A、C两地.求A、C两地之间的距离(精确到0.1海里).