题目内容
11.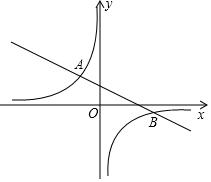 如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.(1)求m,k的值;
(2)过点M(a,0)(a<0)作x轴的垂线交直线AB于点P,交反比例函数y=$\frac{k}{x}$(k≠0)于点Q,若PQ=4QM,求实数a的值.
分析 (1)将点A、B坐标代入反比例函数解析式得出关于m、k的方程组,解之可得;
(2)根据A、B坐标求得直线解析式,由M(a,0)得出yP=-$\frac{1}{2}$a+2、yQ=$\frac{-6}{a}$,从而知$PQ=|-\frac{1}{2}a+2+\frac{6}{a}|$,$|QM|=|-\frac{6}{a}|$,根据PQ=4QM建立关于a的方程,解之可得.
解答 解:(1)∵点 A(-2,m+4),点B(6,m)在反比例函数$y=\frac{k}{x}$的图象上.
∴$\left\{\begin{array}{l}m+4=-\frac{k}{2}\\ m=\frac{k}{6}\end{array}\right.$.
∴解得:m=-1,k=-6.
(2)设过A、B两点的一次函数解析式为y=ax+b.
∵A(-2,3),B(6,-1),
∴$\left\{\begin{array}{l}-2k+b=3\\ 6k+b=-1\end{array}\right.$.
解得:$\left\{\begin{array}{l}k=-\frac{1}{2}\\ b=2\end{array}\right.$.
∴过A、B两点的一次函数解析式为$y=-\frac{1}{2}x+2$.
∵过点M(a,0)作x轴的垂线交AB于点P,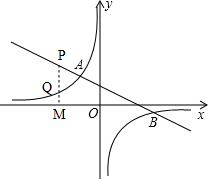
∴点P的纵坐标为:$-\frac{1}{2}a+2$.
又∵过点M(a,0)作x轴的垂线交$y=\frac{-6}{x}$于点Q,
∴点Q的纵坐标为:$\frac{-6}{a}$.
∴$PQ=|-\frac{1}{2}a+2+\frac{6}{a}|$,$|QM|=|-\frac{6}{a}|$.
又∵PQ=4QM且a<0,
∴$-\frac{1}{2}a+2+\frac{6}{a}=-\frac{24}{a}$.
∴a2-4a-60=0.
∴a=-6或a=10.
∵a<0.
∴实数a的值为-6.
点评 此题考查了反比例函数与一次函数的交点问题,熟练掌握待定系数法求函数解析式及两点间的距离公式、解方程的能力是解题的关键.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案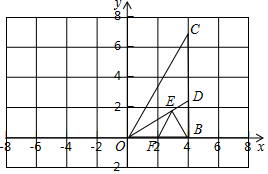 如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$).
如图,Rt△OBC中,OB=4,∠BOC=60°,∠BOC的平分线交BC于D,E、F分别是OD、OB上的动点,BE+EF取到最小值时,E点坐标为(2,$\frac{2\sqrt{3}}{3}$).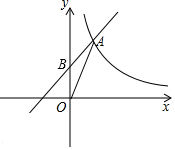 如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.
如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.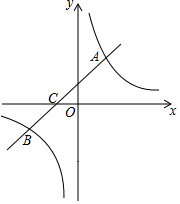 如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).
如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).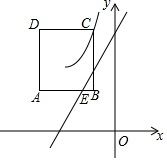 如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=$\frac{1-2m}{x}$(x<0)经过点C.
如图,在平面直角坐标系中,边长为2的正方形ABCD位于第二象限,且AB∥x轴,点B在点C的正下方,双曲线y=$\frac{1-2m}{x}$(x<0)经过点C.