题目内容
16.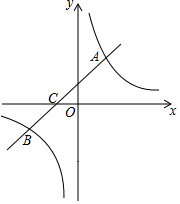 如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).
如图,直线y=$\frac{1}{2}$x+b与双曲线y=$\frac{6}{x}$相交于点A(m,3),与x轴相交于点C,点P是x轴上一点,如果△PAC的面积等于6,那么点P的坐标是(0,0)或(-8,0).
分析 将点A(m,3)代入反比例函数解析式求得点A坐标,在将点A(2,3)代入直线解析式可得b,从而由直线解析式求得点C坐标,设点P(x,0),则PC=|x+4|,根据面积公式求得x的值即可得出答案.
解答 解:将点A(m,3)代入y=$\frac{6}{x}$,得:m=2,
则点A(2,3),
将点A(2,3)代入y=$\frac{1}{2}$x+b,得:1+b=3,即b=2,
∴一次函数解析式为y=$\frac{1}{2}$x+2,
当y=0时,$\frac{1}{2}$x+2=0,解得:x=-4,
∴点C(-4,0),
设点P(x,0),
则PC=|x+4|,
由S△PAC=$\frac{1}{2}$•PC•yA可得$\frac{1}{2}$|x+4|•3=6,
解得:x=0或x=-8,
∴点P的坐标为(0,0)或(-8,0),
故答案为:(0,0)或(-8,0).
点评 本题主要考查反比例函数和一次函数的交点问题,熟练掌握待定系数法求函数解析式及三角形的面积是解题的关键.

练习册系列答案
相关题目
13.为了解某班学生双休户外活动情况,对部分学生参加户外活动的时间进行抽样调查,结果如下表:
则关于“户外活动时间”这组数据的众数、中位数、平均数分别是( )
| 户外活动的时间(小时) | 1 | 2 | 3 | 6 |
| 学生人数(人) | 2 | 2 | 4 | 2 |
| A. | 3、3、3 | B. | 6、2、3 | C. | 3、3、2 | D. | 3、2、3 |
4.若代数式$\frac{2}{x-2}$在实数范围内有意义,则x的取值范围是( )
| A. | x<2 | B. | x≠2 | C. | x>2 | D. | x=2 |
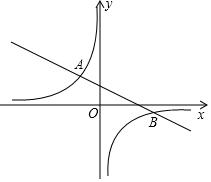 如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.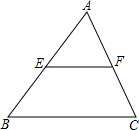 如图,EF为△ABC的中位线,△AEF的面积为6,则四边形EBCF的面积为18.
如图,EF为△ABC的中位线,△AEF的面积为6,则四边形EBCF的面积为18.