题目内容
6.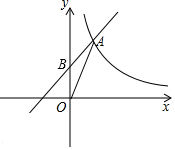 如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.
如图,一次函数y=x+$\frac{3}{2}$的图象反比例函数y=$\frac{k}{x}$的图象在第一象限的一个交点为A(1,m),与y轴交于B点.(1)求反比例函数y=$\frac{k}{x}$的表达式;
(2)若点P在x轴上,且满足S△POB=S△AOB,求此时点P的坐标.
分析 (1)将点A(1,m)代入y=x+$\frac{3}{2}$求得m,即可得出点A坐标,再将其代入反比例函数解析式即可得;
(2)先求得S△AOB,设点P(x,0),则OP=|x|,根据S△POB=S△AOB可得关于x的方程,解之可得.
解答 解:(1)∵一次函数y=x+$\frac{3}{2}$的图象经过点A(1,m),
得m=1+$\frac{3}{2}$=$\frac{5}{2}$,
将(1,$\frac{5}{2}$)代入y=$\frac{k}{x}$,得k=$\frac{5}{2}$,
∴反比例函数的表达式为y=$\frac{5}{2x}$;
(2)由(1)得OB=$\frac{3}{2}$,
∴S△AOB=$\frac{1}{2}$×1×$\frac{3}{2}$=$\frac{3}{4}$,
设点P(x,0),
则OP=|x|,
由S△POB=S△AOB得,$\frac{1}{2}$•|x|•$\frac{3}{2}$=$\frac{3}{4}$,
解得:x=±1,
∴点P的坐标为(-1,0)或(1,0).
点评 本题主要考查反比例函数与一次函数的交点问题,反比例函数与一次函数的交点坐标满足两函数的解析式.也考查了三角形面积公式.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
3.在创建“全国园林城市”期间,郴州市某中学组织共青团员去植树,其中七位同学植树的棵树分别为:3,1,1,3,2,3,2,这组数据的中位数和众数分别是( )
| A. | 3,2 | B. | 2,3 | C. | 2,2 | D. | 3,3 |
 如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为6.
如图,点O是矩形纸片ABCD的对称中心,E是BC上一点,将纸片沿AE折叠后,点B恰好与点O重合.若BE=3,则折痕AE的长为6.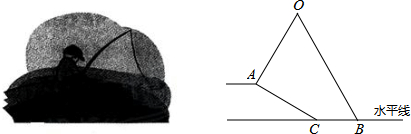
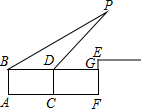 某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下:
某学校组织数学兴趣小组的学生,进行一次课外数学实践探究活动,活动课题:利用直角三角形的边角关系,测量“底部不可以到达的旗杆高度”,活动的方式:两个人一个小组,测量后全班交流研讨,活动工具:测倾器,长度相同的标杆若干,皮尺等测量工具,已知领操台EM距地面的高EF为2m,标杆的长为1.6m,甲乙两人分在一组,测量步骤如下: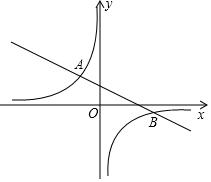 如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.
如图,已知点 A(-2,m+4),点B(6,m)在反比例函数y=$\frac{k}{x}$(k≠0)的图象上.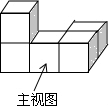 下列是由5个完全相同的正方体组成的立体图形,它的俯视图是( )
下列是由5个完全相同的正方体组成的立体图形,它的俯视图是( )