Question

9．若关于x的一元二次方程（x-2）（x-3）=m有实数根x₁，x₂，且x₁≠x₂．
（1）求m的取值范围；
（2）如果这个方程的两个实根分别为x₁=α，x₂=β，且α＜β，当m＞0时，试比较α，β，2，3的大小，并用“＜”连接；
（3）求二次函数y=（x-x₁）（x-x₂）+m的图象与x轴的交点坐标．

Answer 1

分析 （1）因为一元二次方程（x-2）（x-3）=m有实数根x₁，x₂，所以根的判别式大于0，进而可求出m的取值范围；
（2）令m=0，则函数y=（x-2）（x-3）的图象与x轴的交点分别为（2，0），（3，0），当m＞0，原顶点沿抛物线对称轴向下移动，两个根沿对称轴向两边逐步增，进而可得到：α＜2，β＞3，则α，β，2，3的大小即可求出；
（3）因为一元二次方程可以写成（x-x₁）（x-x₂）=0或者（x-2）（x-3）-m=0，所以y=（x-x₁）（x-x₂）+m可以表示成y=（x-2）（x-3）-m+m，进而可求出y=（x-x₁）（x-x₂）+m的图象与x轴的交点坐标．

解答 解：
（1）∵关于x的一元二次方程（x-2）（x-3）=m有实数根x₁，x₂，且x₁≠x₂，
∴△＞0，
即25-4×1×（6-m）＞0，
解得：m＞-$\frac{1}{4}$；
（2）令m=0，
则函数y=（x-2）（x-3）的图象与x轴的交点分别为（2，0），（3，0），
故此函数的图象为：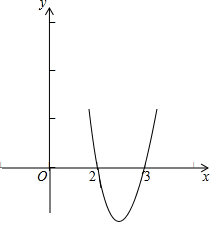

∵m＞0，
∴原顶点沿抛物线对称轴向下移动，两个根沿对称轴向两边逐步增大，
∴α＜2，β＞3，
∴α＜2＜3＜β；
（3）因为一元二次方程（x-2）（x-3）=m有实数根x₁，x₂，且x₁≠x₂．
所以该一元二次方程可以写成（x-x₁）（x-x₂）=0或者（x-2）（x-3）-m=0，
即：（x-x₁）（x-x₂）=（x-2）（x-3）-m，
所以y=（x-x₁）（x-x₂）+m可以表示成y=（x-2）（x-3）-m+m，
即：y=（x-2）（x-3），
求二次函数的图象与x轴的交点坐标为（2，0）和（3，0）．

点评 本题考查了抛物线和x轴交点坐标问题、根的判别式的运用以及根与系数的关系，本题的综合性较强，需要学生有很好的变通能力，熟记根与系数的关系是解题的关键．