题目内容
1. 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A、B两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象交于A、B两点.(1)利用图中的条件,求反比例函数和一次函数的解析式.
(2)求△AOB的面积.
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
分析 (1)将点A代入y=$\frac{m}{x}$可得反比例函数解析式,将点B(-1,n)代入可得n的值,即可得点B的坐标,由A、B坐标可得直线的解析式;
(2)求得直线与x轴的交点坐标,利用割补法可得三角形的面积;
(3)由直线位于双曲线上方时对应的x的范围即可得答案.
解答 解:(1)把A(2,1)代入y=$\frac{m}{x}$,得:m=2,
∴反比例函数的解析式为y=$\frac{2}{x}$,
把B(-1,n)代入y=$\frac{2}{x}$,得:n=-2,即B(-1,-2),
将点A(2,1)、B(-1,-2)代入y=kx+b,
得:$\left\{\begin{array}{l}{2k+b=1}\\{-k+b=-2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴一次函数的解析式为y=x-1;
(2)在一次函数y=x-1中,令y=0,得:x-1=0,解得:x=1,
则S△AOB=$\frac{1}{2}$×1×1+$\frac{1}{2}$×1×2=$\frac{3}{2}$;
(3)由图象可知,当x>2或-1<x<0时,一次函数的值大于反比例函数的值.
点评 本题主要考查反比例函数与一次函数相交问题,熟练掌握待定系数法求函数解析式及割补法求三角形的面积是解题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
12.实数$\sqrt{9}$的平方根( )
| A. | 3 | B. | -3 | C. | ±3 | D. | ±$\sqrt{3}$ |
10.已知二次函数y=ax2+bx+c的图象过点A(1,2),B(3,2),C(5,7).若点M(-2,y1),N(-1,y2),K(8,y3)也在二次函数y=ax2+bx+c的图象上,则下列结论正确的是( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y1<y2 | D. | y2<y1<y3 |
 如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③.
如图,是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:①abc<0;②b+2a=0;③ac<$\frac{1}{4}$b2;④3a+c>0.其中正确的命题是②③.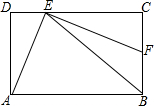 如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.
如图,在矩形ABCD中,BE平分∠ABC且交CD于点E,EF⊥AE且交BC于点F,求证:AE=EF.