题目内容
8.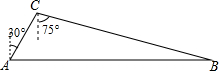 如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.
如图,油库C位于油井A北偏东30°方向,输油管道AC的长为50千米,新建油井B位于C南偏东75°方向,且位于A的正东方向.(1)求∠ABC的度数;
(2)求油井A、B之间的距离(结果精确到1千米).(参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41)
分析 (1)根据已知条件得到∠ACB=∠MCA+∠BCM=105°,根据三角形的内角和即可得到结论;
(2)过C作CD⊥AC交AB于D根据调整以及得到CD=DB,解直角三角形即可得到结论.
解答  解:(1)由题意得:∠NAC=∠MCA=30°,∠CAB=60°,
解:(1)由题意得:∠NAC=∠MCA=30°,∠CAB=60°,
∴∠ACB=∠MCA+∠BCM=105°,
在△ACB中,∠CAB=∠ABC+∠ACB=180°,
∴∠ABC=180°-60°-105°=15°;
(2)过C作CD⊥AC交AB于D,
∴∠ACB=90°,
∵∠CAB=60°,
∴∠ADC=30°,
∴AD=2AC=2×50=100(海里)
∵∠ADC=∠ABC+∠DCB,
∴∠DBC=∠DCB=15°,
∴CD=DB,
在Rt△ACD中,∠ACB=90°,∠CAD=60°,
∴tan∠CAD=$\frac{CD}{AC}$,
∴CD=AC•tan∠CAD=50×$\sqrt{3}$=50$\sqrt{3}$
∵AB=AD+BD,
∴AB=100+50$\sqrt{3}$≈187(千米),
答:油井AB之间的距离约为187千米.
点评 本题考查的是解直角三角形的应用-方向角问题,根据题意作出辅助线,利用直角三角形的性质求解是解答此题的关键.

练习册系列答案
相关题目
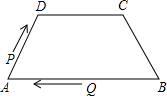 如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发,以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动,在运动期间,当四边形PQBC为平行四边形时,运动时间为3秒.
 如图,在△ABC中,∠ACB=90,DE是AB的垂直平分线,∠CAE:∠EAB=4:1.
如图,在△ABC中,∠ACB=90,DE是AB的垂直平分线,∠CAE:∠EAB=4:1.