题目内容
19.在?ABCD中,对角线AC、BD交于点O,设$\overrightarrow{AB}=\overrightarrow m$,$\overrightarrow{AD}=\overrightarrow n$,如果用向量$\overrightarrow m$、$\overrightarrow n$表示向量$\overrightarrow{AO}$,那么$\overrightarrow{AO}$=$\frac{1}{2}$$\overrightarrow{m}$+$\frac{1}{2}$$\overrightarrow{n}$.分析 首先根据题意画出图形,然后由四边形ABCD是平行四边形,求得$\overrightarrow{AC}$,继而求得答案.
解答  解:如图,四边形ABCD是平行四边形,
解:如图,四边形ABCD是平行四边形,
∴$\overrightarrow{DC}$=$\overrightarrow{AB}=\overrightarrow m$,AO=$\frac{1}{2}$AC,
∵$\overrightarrow{AD}=\overrightarrow n$,
∴$\overrightarrow{AC}$=$\overrightarrow{AD}$+$\overrightarrow{DC}$=$\overrightarrow{m}$+$\overrightarrow{n}$,
∴$\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{m}$+$\overrightarrow{n}$)=$\frac{1}{2}$$\overrightarrow{m}$+$\frac{1}{2}$$\overrightarrow{n}$.
故答案为:$\frac{1}{2}$$\overrightarrow{m}$+$\frac{1}{2}$$\overrightarrow{n}$.
点评 此题考查了平面向量的知以及平行四边形的性质.注意掌握三角形法则与平行四边形法则的应用是解此题的关键.

练习册系列答案
相关题目
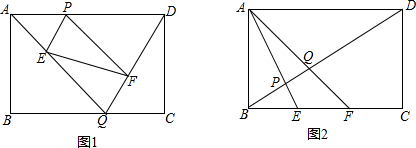
 如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )
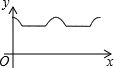
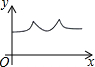
如图,矩形ABCD中,AB=6cm,BC=10cm,O是矩形对角线交点,线段OP⊥AD,且OP=4cm,线段OP从图中位置开始,绕点O顺时针旋转一周,线段OP在矩形内部部分(包括端点)的长度y(cm)与点P走过的路程 x(cm)的函数关系式可能是( )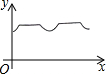
 如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.
如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米. 在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.
在平面直角坐标系xOy中,点A(2,0),点P(1,m)(m>0)和点Q关于x轴对称.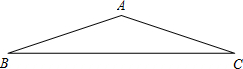 如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为
如图,已知在△ABC中,AB=AC,tan∠B=$\frac{1}{3}$,将△ABC翻折,使点C与点A重合,折痕DE交边BC于点D,交边AC于点E,那么$\frac{BD}{DC}$的值为 .
.