题目内容
5. 如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.
如图,圆柱形玻璃板,高为12cm,底面周长为18cm,在杯内离杯底4cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的A处,则蚂蚁到达蜂蜜的最短距离( )cm.| A. | 14 | B. | 15 | C. | 16 | D. | 17 |
分析 在侧面展开图中,过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则AP+PC就是蚂蚁到达蜂蜜的最短距离,求出A′Q,CQ,根据勾股定理求出A′C即可.
解答  解:沿过A的圆柱的高剪开,得出矩形EFGH,
解:沿过A的圆柱的高剪开,得出矩形EFGH,
过C作CQ⊥EF于Q,作A关于EH的对称点A′,连接A′C交EH于P,连接AP,则
AP+PC就是蚂蚁到达蜂蜜的最短距离,
∵AE=A′E,A′P=AP,
∴AP+PC=A′P+PC=A′C,
∵CQ=$\frac{1}{2}$×18cm=9cm,A′Q=12cm-4cm+4cm=12cm,
在Rt△A′QC中,由勾股定理得:A′C=$\sqrt{1{2}^{2}+{9}^{2}}$=15cm,
故选(B)
点评 本题考查了平面展开-最短路径问题,同时也考查了学生的空间想象能力.将图形侧面展开,利用轴对称的性质和勾股定理进行计算是解题的关键.

练习册系列答案
相关题目
15.若x>y,则下列式子中错误的是( )
| A. | x-2>y-2 | B. | x+3>y+3 | C. | $\frac{x}{3}$>$\frac{y}{3}$ | D. | -5x>-5y |
11.红光运输队欲用A,B,C三种型号的汽车共80辆为某企业一次性将700吨货物从M地运往N地(要求每种型号的汽车都满载),三种型号的汽车的载重量及应获取的运费如表:
设派用A型汽车x辆,B型汽车y辆,红光运输队应获取的总运费为w元.
(1)用含x、y的代数式表示派用的C型汽车的辆数(80-x-y);
(2)求y关于x的函数关系式并直接写出x的取值范围;
(3)求w关于x的函数关系式;
(4)若红光运输队获取的总运费为18600元,请问他们的派车方案是怎样的?
| 汽车型号 | A型 | B型 | C型 |
| 载重量(吨) | 8 | 10 | 12 |
| 运费(元) | 220 | 260 | 280 |
(1)用含x、y的代数式表示派用的C型汽车的辆数(80-x-y);
(2)求y关于x的函数关系式并直接写出x的取值范围;
(3)求w关于x的函数关系式;
(4)若红光运输队获取的总运费为18600元,请问他们的派车方案是怎样的?
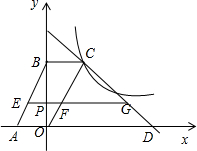 如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.
如图,在平面直角坐标系中,四边形ABCO是平行四边形,点O为坐标原点,点A的坐标为(-2,0),点B在y轴的正半轴上,点C在双曲线y=-$\frac{8}{x}$上,直线y=-x+m经过点C,交x轴于点D.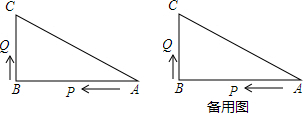
 如图,抛物线y=ax2+bx+c与直线y=kx+4交于A(1,m),B(4,8),与x轴交于原点及C点.
如图,抛物线y=ax2+bx+c与直线y=kx+4交于A(1,m),B(4,8),与x轴交于原点及C点. 如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC向左平移2个单位后得到△A1B1C1.
如图,在边长为1的正方形网格中,△ABC的顶点均在格点上,点A、B的坐标分别是A(4,3)、B(4,1),把△ABC向左平移2个单位后得到△A1B1C1.