��Ŀ����
16����ͼ����֪��ABC�У���B=90�㣬AB=16cm��BC=12cm��P��Q�ǡ�ABC���ϵ��������㣬���е�P�ӵ�A��ʼ��A��B�����˶������ٶ�Ϊÿ��1cm����Q�ӵ�B��ʼ��B��C��A�����˶������ٶ�Ϊÿ��2cm������ͬʱ�������������ʱ��Ϊt�룮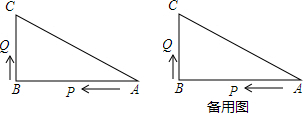
��1������4�����PQ�ij���
��2������Q�ڱ�BC���˶�ʱ�����������Ӻ�PQB���ABC���ƣ�
��3������Q�ڱ�CA���˶�ʱ������ʹ��APQ��Ϊ���������ε��˶�ʱ�䣮
���� ��1�������ж���Q��λ�ã����BQ��BP���ù��ɶ������ɣ�
��2�����������Σ��ٵ�PQ��ACʱ����PBQ�ס�ABC���ڵ���BPQ=��Cʱ���ɡ�B=��B���á�BPQ�ס�BCA���г����̼��ɽ�����⣮
��3��������������ͼ1�У���PA=PQʱ����PM��AC��M������cosA=$\frac{AM}{AP}$=$\frac{AB}{AC}$���г����̼��ɣ�����ͼ2�У���AP=AQʱ������ͼ3�У���QP=QAʱ����QM��AB��M��
����cosA=$\frac{AM}{AQ}$=$\frac{AB}{AC}$���з��̼��ɣ�
��� �⣺��1��t=4ʱ��BQ=2��4=8��12����ʱQ��BC���ϣ�AP=4��1=4��
��Rt��PBQ�У��ߡ�B=90�㣬BQ=8��BP=AB-AP=16-4=12��
��PQ=$\sqrt{B{Q}^{2}+B{P}^{2}}$=$\sqrt{{8}^{2}+1{2}^{2}}$=4$\sqrt{13}$��
��2���ٵ�PQ��ACʱ����PBQ�ס�ABC����$\frac{PB}{AB}$=$\frac{BQ}{BC}$��
��$\frac{16-t}{16}$=$\frac{2t}{12}$��
��t=$\frac{48}{11}$��
�ڵ���BPQ=��Cʱ��
�ߡ�B=��B�����BPQ�ס�BCA��
��$\frac{BP}{BC}$=$\frac{BQ}{BA}$��
��$\frac{16-t}{12}$=$\frac{2t}{16}$��
��t=$\frac{32}{5}$��
��t=$\frac{48}{11}$���$\frac{32}{5}$��ʱ����PQB���ABC���ƣ�
��3������ͼ1�У���PA=PQʱ����PM��AC��M��
��PA=PQ��PM��AQ��
��AM=MQ��
��cosA=$\frac{AM}{AP}$=$\frac{AB}{AC}$��
��Rt��ABC��AC=$\sqrt{B{C}^{2}+A{B}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20��
��AP=t��AM=MQ=$\frac{1}{2}$��32-2t��=16-t��
��$\frac{16-t}{t}$=$\frac{4}{5}$��
��t=$\frac{80}{9}$
����ͼ2�У���AP=AQʱ��
t=32-2t�����t=$\frac{32}{3}$��
����ͼ3�У���QP=QAʱ����QM��AB��M��
��cosA=$\frac{AM}{AQ}$=$\frac{AB}{AC}$��
��$\frac{\frac{t}{2}}{32-2t}$=$\frac{4}{5}$��
��t=$\frac{256}{21}$��
����������t=$\frac{80}{9}$��$\frac{32}{3}$��$\frac{256}{21}$��ʱ����APQ�ǵ��������Σ�
���� ���⿼�������������ۺ��⡢���������ε��ж������ʡ����ɶ�����������Ǻ�����֪ʶ������Ĺؼ���ѧ��������ۣ�����©�⣬ѧ�����÷��̵�����˼�����⣬�����п��������ͣ�

 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д� ��ABF����CDM=
��ABF����CDM= ��ABF, ��CDM��
��ABF, ��CDM��
 ��ͼ���ھ���ABCD�У�AB=4��AD=$\sqrt{3}$����E��AB���е㣬���߶�DC��ÿ��1����λ���ȵ��ٶ�������DC����ƽ����D��C�䣬���ƶ�ʱ��Ϊt�룬����D��E���ӳ�����C��B���ӳ����ڵ�F������AF��
��ͼ���ھ���ABCD�У�AB=4��AD=$\sqrt{3}$����E��AB���е㣬���߶�DC��ÿ��1����λ���ȵ��ٶ�������DC����ƽ����D��C�䣬���ƶ�ʱ��Ϊt�룬����D��E���ӳ�����C��B���ӳ����ڵ�F������AF�� ��ͼ��һ�������������ͼ��ͼ�гߴ絥λ��cm��������ͼ����ʾ���ݼ������������ı������
��ͼ��һ�������������ͼ��ͼ�гߴ絥λ��cm��������ͼ����ʾ���ݼ������������ı������ ��ͼ��Բ���β����壬��Ϊ12cm�������ܳ�Ϊ18cm���ڱ����뱭��4cm�ĵ�C����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����4cm�������Ե�A���������ϵ�����۵���̾��루������cm��
��ͼ��Բ���β����壬��Ϊ12cm�������ܳ�Ϊ18cm���ڱ����뱭��4cm�ĵ�C����һ�η��ۣ���ʱһֻ���������ڱ���ڣ��뱭����4cm�������Ե�A���������ϵ�����۵���̾��루������cm��