题目内容
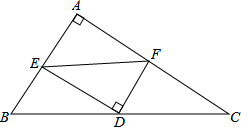 如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.考点:全等三角形的判定与性质,等腰三角形的判定与性质,勾股定理
专题:
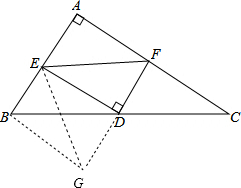
分析:延长FD至点G,使得DG=DF,连接BG,EG,易证△CDF≌△BDG,可得BG=CF=4,∠C=∠DBG,可证明∠ABG=90°,再根据等腰三角形底边三线合一性质可得EF=EG,即可求得EF的长,即可解题.
解答:解:延长FD至点G,使得DG=DF,连接BG,EG,
∵在△CDF和△BDG中,
,
∴△CDF≌△BDG(SAS),
∴BG=CF=4,∠C=∠DBG,
∵∠C+∠ABC=90°,
∴∠DBG+∠ABC=90°,即∠ABG=90°,
∵DE⊥FG,DF=DG,
∴EF=EG=
=5.

∵在△CDF和△BDG中,
|
∴△CDF≌△BDG(SAS),
∴BG=CF=4,∠C=∠DBG,
∵∠C+∠ABC=90°,
∴∠DBG+∠ABC=90°,即∠ABG=90°,
∵DE⊥FG,DF=DG,
∴EF=EG=
| BG2+BE2 |
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△CDF≌△BDG是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
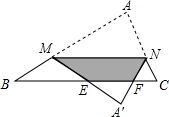 已知一三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C都为锐角,M为AB边上一动点(M与点A、B不重合),过点M作MN∥BC,交AC于点N.将△AMN沿MN折叠,使点A落在BC的下方.设MN=x,△A′MN与四边形BCNM重叠部分面积为y.
已知一三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C都为锐角,M为AB边上一动点(M与点A、B不重合),过点M作MN∥BC,交AC于点N.将△AMN沿MN折叠,使点A落在BC的下方.设MN=x,△A′MN与四边形BCNM重叠部分面积为y. 如图,已知AB切⊙O于点A,OB⊥AC于点C,交⊙O于点D,连接AD,求证:∠1=∠2.
如图,已知AB切⊙O于点A,OB⊥AC于点C,交⊙O于点D,连接AD,求证:∠1=∠2.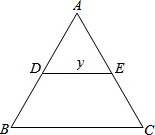 如图,△ABC中,AB=8,AC=6,BC=9,如果动点D以每秒2个单位长的速度,从点B出发沿边BA向点A运动,直线DE∥BC,交AC于E.记x秒时DE的长度是y,写出y关于x的函数关系式.并画出它的图象.
如图,△ABC中,AB=8,AC=6,BC=9,如果动点D以每秒2个单位长的速度,从点B出发沿边BA向点A运动,直线DE∥BC,交AC于E.记x秒时DE的长度是y,写出y关于x的函数关系式.并画出它的图象.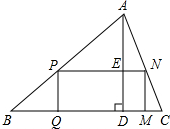 如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E.设BC=48,AD=16,PQ:PN=5:9,求矩形PQMN的面积.
如图,在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在BC上,AD交PN于点E.设BC=48,AD=16,PQ:PN=5:9,求矩形PQMN的面积.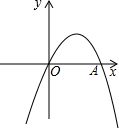 如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点.
如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点.