题目内容
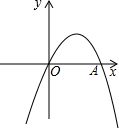 如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点.
如图,二次函数y=-x2+(1-2k)x+k+1的图象与x轴相交于点O,A两点.(1)求这个二次函数的解析式;
(2)在这条抛物线的对称轴的右边的图象上有一个点B1使得锐角三角形AOB的面积等于3,求点B的坐标.
(3)对于(2)中的点B,在抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据二次函数经过点O,即可求得k的值,即可解题;
(2)易求得该二次函数的对称轴,设点B(a,b),即可求得b的值,根据b的值即可求得a的值,即可解题;
(3)设符合题意的点P坐标为(m,n),易得∠AOB=45°,即可求得∠AOP=45°,可得m=-n,将点P代入即可求得m、n的值,即可解题.
(2)易求得该二次函数的对称轴,设点B(a,b),即可求得b的值,根据b的值即可求得a的值,即可解题;
(3)设符合题意的点P坐标为(m,n),易得∠AOB=45°,即可求得∠AOP=45°,可得m=-n,将点P代入即可求得m、n的值,即可解题.
解答:解:(1)∵二次函数y=-x2+(1-2k)x+k+1的图象经过点O,
∴将O点代入得:k+1=0,
∴k=-1,
∴二次函数的解析式为y=-x2+3x;
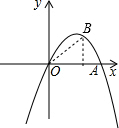
(2)如图,在抛物线上找到点B,作BA⊥x轴,连接OB.
∵y=-x2+3x=-(x-
)2+
,
∴对称轴是直线x=
,令y=0,则-x2+3x=0,
∴x1=-,x2=3,
∴点A(3,0),
设点B(a,b),
∴
×3×|b|=3,
∴b=±2,
当b=-2时,△AOB是钝角三角形,不符合题意,舍去,
当b=2时,即2=-a2+3a,解得:a1=1,a2=2.
∵当a=1时,点B在对称轴左边,不符合题意,舍去,
∴a=2,
∴点B坐标为(2,2);
(3)在抛物线上存在点P,使∠POB=90°,
设符合题意的点P坐标为(m,n)
∵B的坐标为(2,2),∴∠AOB=45°,
∴∠AOP=45°,且点P必在x轴的下方,
∴m=-n,
即-m2+3m=-m,解得:m1=0,(舍去),m2=4,
故点P坐标为(4,-4).
∴将O点代入得:k+1=0,
∴k=-1,
∴二次函数的解析式为y=-x2+3x;
(2)如图,在抛物线上找到点B,作BA⊥x轴,连接OB.

∵y=-x2+3x=-(x-
| 3 |
| 2 |
| 9 |
| 4 |
∴对称轴是直线x=
| 3 |
| 2 |
∴x1=-,x2=3,
∴点A(3,0),
设点B(a,b),
∴
| 1 |
| 2 |
∴b=±2,
当b=-2时,△AOB是钝角三角形,不符合题意,舍去,
当b=2时,即2=-a2+3a,解得:a1=1,a2=2.
∵当a=1时,点B在对称轴左边,不符合题意,舍去,
∴a=2,
∴点B坐标为(2,2);
(3)在抛物线上存在点P,使∠POB=90°,
设符合题意的点P坐标为(m,n)
∵B的坐标为(2,2),∴∠AOB=45°,
∴∠AOP=45°,且点P必在x轴的下方,
∴m=-n,
即-m2+3m=-m,解得:m1=0,(舍去),m2=4,
故点P坐标为(4,-4).
点评:本题考查了二次函数的综合应用,考查了三角形面积计算,考查了一元二次方程的求解,本题中求得点B的值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
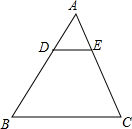 如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是
如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是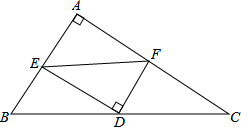 如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长. 如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度.
如图所示,点C、D为线段AB的三等分点,点E为线段AC的中点,若EC=3,求线段AB的长度. 已知B(10,0),OA=5,sin∠AOB=
已知B(10,0),OA=5,sin∠AOB=