题目内容
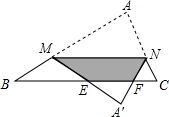 已知一三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C都为锐角,M为AB边上一动点(M与点A、B不重合),过点M作MN∥BC,交AC于点N.将△AMN沿MN折叠,使点A落在BC的下方.设MN=x,△A′MN与四边形BCNM重叠部分面积为y.
已知一三角形纸片ABC,面积为25,BC边的长为10,∠B和∠C都为锐角,M为AB边上一动点(M与点A、B不重合),过点M作MN∥BC,交AC于点N.将△AMN沿MN折叠,使点A落在BC的下方.设MN=x,△A′MN与四边形BCNM重叠部分面积为y.(1)试求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)当x为何值时,重叠部分的面积y最大?最大值为多少?
考点:翻折变换(折叠问题),二次函数的最值
专题:
分析:(1)如图,作辅助线;首先求出△ABC的高;运用相似三角形的性质求出A′P(用x表示),进而求出△A′MN、△A′EF的面积,问题即可解决.
(2)借助二次函数的性质,直接求出y的最大值,即可解决问题.
(2)借助二次函数的性质,直接求出y的最大值,即可解决问题.
解答: 解:(1)如图,连接AA′,分别交MN、EF于点P、Q;
解:(1)如图,连接AA′,分别交MN、EF于点P、Q;
则AA′⊥MN、PA′⊥EF;AP=A′P;
设PQ=λ,则AP=AQ-λ,A′Q=AQ-2λ;
∵MN∥BC,而AQ⊥MN,
∴AQ⊥BC;
∵面积为25,BC边的长为10,
∴
×10×AQ=25,AQ=5;
∵MN∥BC,
∴△AMN∽△ABC,
∴MN:BC=AP:AQ,即x:10=(5-λ):5,
∴λ=5-
x,A′P=5-λ=
x;A′Q=x-5;
设△A′MN、△A′EF的面积分别为α、β、;
则α=
x•
x=
x2;
∵EF∥MN,
∴△A′EF∽△A′MN,
∴
=(
)2,
∴β=(x-5)2,
∴y=α-β=-
x2+10x-25.
(2)由(1)知:y=-
x2+10x-25,
∵a=-
<0,
∴该函数图象开口向下,当x=-
=
,
y取得最大值,ymax=
=
.
 解:(1)如图,连接AA′,分别交MN、EF于点P、Q;
解:(1)如图,连接AA′,分别交MN、EF于点P、Q;则AA′⊥MN、PA′⊥EF;AP=A′P;
设PQ=λ,则AP=AQ-λ,A′Q=AQ-2λ;
∵MN∥BC,而AQ⊥MN,
∴AQ⊥BC;
∵面积为25,BC边的长为10,
∴
| 1 |
| 2 |
∵MN∥BC,
∴△AMN∽△ABC,
∴MN:BC=AP:AQ,即x:10=(5-λ):5,
∴λ=5-
| 1 |
| 2 |
| 1 |
| 2 |
设△A′MN、△A′EF的面积分别为α、β、;
则α=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∵EF∥MN,
∴△A′EF∽△A′MN,
∴
| β |
| α |
| x-5 | ||
|
∴β=(x-5)2,
∴y=α-β=-
| 3 |
| 4 |
(2)由(1)知:y=-
| 3 |
| 4 |
∵a=-
| 3 |
| 4 |
∴该函数图象开口向下,当x=-
| 10 | ||
2(-
|
| 20 |
| 3 |
y取得最大值,ymax=
4×(-
| ||
4×(-
|
=
| 25 |
| 3 |
点评:该题主要考查了翻折变换及其性质的应用问题;解题的关键是根据翻折变换的性质准确找出图形中隐含的等量关系,灵活运用相似三角形的性质等几何知识点来分析、判断、推理或解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知AB:AC=1:3,AC:AD=1:4,且AB+AC+AD=40,则AB=
如图,已知AB:AC=1:3,AC:AD=1:4,且AB+AC+AD=40,则AB=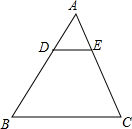 如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是
如图,△在ABC中,DE∥BC,若DE:BC=1:3,则△ADE与△ABC的周长之比是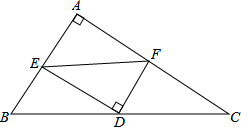 如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.
如图,△ABC中,∠A=90°,D为斜边BC的中点,E、F分别为AB、AC上的点,且DE⊥DF.若BE=3,CF=4,试求EF的长.