题目内容
7.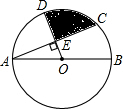 如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )
如图,⊙O的直径AB=4cm,AC是⊙O的弦,∠BAC=30°,点D在⊙O上,OD⊥AC于E,则阴影部分的面积为( )| A. | $\frac{20π-15\sqrt{3}}{30}$cm2 | B. | $\frac{24π-15\sqrt{3}}{30}$cm2 | C. | $\frac{20π-18\sqrt{3}}{30}$cm2 | D. | $\frac{20π-15\sqrt{3}}{20}$cm2 |
分析 此题可用锐角三角函数先求出AE、EO的值,进而用扇形的面积公式及三角形的面积公式即可求出阴影部分的面积.
解答 解:∵OD⊥AC于E,∠BAC=30°,AB=4cm,
∴∠AOE=∠AEO-∠BAC=90°-30°=60°,
AO=2,则AE=cos30°×AO=$\sqrt{3}$cm,
∴EO=1.
∵S阴影=S扇形AOD-S△AEO=$\frac{60π×{2}^{2}}{360}$-$\frac{1}{2}\sqrt{3}$×1,
∴S阴影=$\frac{20π-15\sqrt{3}}{30}$cm2.
故选A.
点评 本题主要考查解直角三角形、扇形和三角形的面积公式,解题的关键是看出S阴影=S扇形AOD-S△AEO.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
15.如图,是一个正六棱柱的主视图和左视图,则图中的a=( )


| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 2 | D. | 1 |
12. 如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
 如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )
如图,已知菱形ABCD的对角线AC,BD的长分别为6,8,AE⊥BC,垂足为点E,则AE的长是( )| A. | $5\sqrt{3}$ | B. | 2$\sqrt{5}$ | C. | $\frac{48}{5}$ | D. | $\frac{24}{5}$ |
16.5的绝对值是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | $\frac{1}{5}$ |
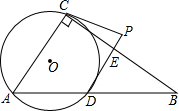 如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.
如图,Rt△ABC中,∠ACB=90°,过A、C两点作⊙O,交边AB于D,PC、PD为⊙O的切线.