题目内容
19．
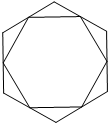如图，顺次连接一个正六边形各边的中点，所得图形仍是正六边形．若大正六边形的面积为S1，小正六边形的面积为S2，则$\frac{{S}_{1}}{{S}_{2}}$的值是$\frac{4}{3}$．
分析 设大正六边形的边长为a，根据正六边形的性质得小正六边形的边长=$\frac{\sqrt{3}}{2}$a，由于所有正六边形都相似，于是得到面积比等于边长比的平方，由此得到结果．
解答 解：设大正六边形的边长为a，
根据正六边形的性质得小正六边形的边长=$\frac{\sqrt{3}}{2}$a，
∵所有正六边形都相似，
∴$\frac{{S}_{1}}{{S}_{2}}$=（$\frac{a}{\frac{\sqrt{3}}{2}a}$）2=$\frac{4}{3}$，
故答案为：$\frac{4}{3}$．
点评 本题考查的是正多边形和圆，熟知正六边形的性质是解答此题的关键．
练习册系列答案
相关题目
13．
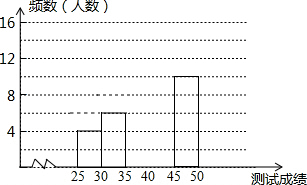为了提高学生书写汉字的能力．增强保护汉字的意识，我区举办了“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
请结合图表完成下列各题：
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
为了提高学生书写汉字的能力．增强保护汉字的意识，我区举办了“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：| 组别 | 成绩x分 | 频数（人数） |
| 第1组 | 25≤x＜30 | 4 |
| 第2组 | 30≤x＜35 | 6 |
| 第3组 | 35≤x＜40 | 14 |
| 第4组 | 40≤x＜45 | a |
| 第5组 | 45≤x＜50 | 10 |
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
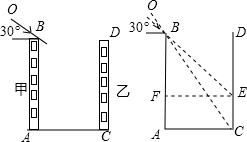棕北中学暑假期间将进行校园外貌环境改造．如图为校园内的两幢教学楼，它们的高AB=CD=35m，它们之间的水平距离AC=30m，现工人现需了解甲楼对乙楼的采光的影响情况，当太阳光与水平线的夹角为30°角时，求EC的高度．
7．下列图形中，既是轴对称图形又是中心对称图形的是（ ）
| A． | 矩形 | B． | 平行四边形 | C． | 等腰三角形 | D． | 直角三角形 |
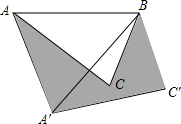如图，在△ABC中，AB=4，将△ABC绕点B按逆时针方向旋转45°后得到△A′BC′，则阴影部分的面积为4$\sqrt{2}$．
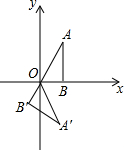如图，点B在x轴上，∠ABO=90°，∠A=30°，OA=4，将△OAB绕点O按顺时针方向旋转120°得到△OA′B′，则点A′的坐标是（2，-2$\sqrt{3}$）．
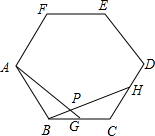如图，点G，H分别是正六边形ABCDEF的边BC，CD上的点，且BG=CH，AG交BH于点P．（1）求证：△ABG≌△BCH；
9．若直线y=$\frac{1}{2}$x+b与y=ax-1相交于点（1，-2），则a+b=（ ）
| A． | -$\frac{7}{2}$ | B． | -$\frac{1}{2}$ | C． | -2 | D． | -$\frac{9}{2}$ |