题目内容
18.先化简,再求值:$\frac{x+1}{x-2}$÷(x+2+$\frac{3}{x-2}$),其中x=$\sqrt{2}$-1.分析 先根据分式混合运算的法则把原式进行化简,再将x的值代入进行计算即可.
解答 解:原式=$\frac{x+1}{x-2}$÷$\frac{(x+2)(x-2)+3}{x-2}$
=$\frac{x+1}{x-2}$•$\frac{x-2}{(x+1)(x-1)}$
=$\frac{1}{x-1}$,
将x=$\sqrt{2}$-1代入得:$\frac{1}{\sqrt{2}-2}$=$-\frac{\sqrt{2}+2}{2}$.
点评 本题考查了分式的化简求值、二次根式的化简.解题的关键是对分式的分子、分母要因式分解.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
13.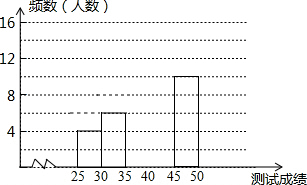 为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
 为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 6 |
| 第3组 | 35≤x<40 | 14 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
3. 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
 如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )
如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10,8),E是BC边上一点,将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=$\frac{k}{x}$的图象与边AB交于点F,则线段AF的长为( )| A. | $\frac{15}{4}$ | B. | 2 | C. | $\frac{15}{8}$ | D. | $\frac{3}{2}$ |
7.下列图形中,既是轴对称图形又是中心对称图形的是( )
| A. | 矩形 | B. | 平行四边形 | C. | 等腰三角形 | D. | 直角三角形 |
 如图,已知m∥n,将一块等边三角形ABC纸板放置在平行线之间,则∠1-∠2等于60度.
如图,已知m∥n,将一块等边三角形ABC纸板放置在平行线之间,则∠1-∠2等于60度.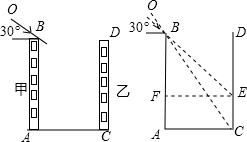 棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度.
棕北中学暑假期间将进行校园外貌环境改造.如图为校园内的两幢教学楼,它们的高AB=CD=35m,它们之间的水平距离AC=30m,现工人现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°角时,求EC的高度.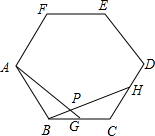 如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;