题目内容
如图1,△ABC中,AB=AC,AD⊥BC交BC于点D,点E在AB边上,点F在AC边的延长线上,连接EF交BC于点M,交AD于点N,∠AEF=2∠F,EM=FM.
(1)求证:∠B=
∠F.
(2)如图2,过点A作AH⊥EF于H,若AH=5,△AEN的面积为15,求线段CF的长.

(1)求证:∠B=
| 3 |
| 2 |
(2)如图2,过点A作AH⊥EF于H,若AH=5,△AEN的面积为15,求线段CF的长.

考点:全等三角形的判定与性质,等腰三角形的判定与性质
专题:
分析:(1)过点E作EG∥AC交BC于点G,就可以得出∠BGE=∠BCA,∠GEM=∠F,就有∠AEG=3∠F=∠B+∠BGE而得出结论;
(2)如图2,作EL∥BC交AC于L,连结NL,就可以得出∠AEL=∠ALE=∠B=∠ACB=
∠F,∠LEN=2∠F-
∠F=
∠F,就可以得出∠LNF=∠F,就有LN=LF=EN.由EG=EB=CF=LC就可以求出结论.
(2)如图2,作EL∥BC交AC于L,连结NL,就可以得出∠AEL=∠ALE=∠B=∠ACB=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
解答: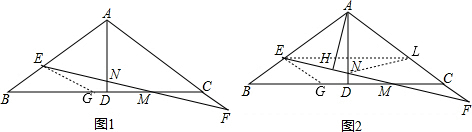 解:(1)如图1,过点E作EG∥AC交BC于点G,
解:(1)如图1,过点E作EG∥AC交BC于点G,
∴∠BGE=∠BCA,∠GEM=∠F,
∵∠AEF=2∠F,
∴∠GEM+∠AEF=∠F+2∠F=3∠F.
即∠AEG=3∠F.
∵AB=AC,
∴∠B=∠BCA,
∴∠BGE=∠B.
∵∠AEG=∠B+∠BGE,
∴∠AEG=2∠B,
∴3∠F=2∠B,
∴∠B=
∠F;
(2)如图2,作EL∥BC交AC于L,连结NL
∴∠AEL=∠ALE=∠B=∠ACB=
∠F.
∴∠LEN=2∠F-
∠F=
∠F.
∵EG∥AC,EL∥BC,
∴四边形EGCL是平行四边形,
∴EG=LC.
在△EGM和△FCM中,
,
∴△EGM≌△FCM(ASA),
∴EG=CF,
∴LC=CF.
∴CF=
LF.
∵∠AEL=∠ALE,
∴AE=AL.
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.
在△EAN和△LAN中
,
∴△EAN≌△LAN(SAS),
∴EN=LN.
∴∠LEN=∠ELN=
∠F..
∵∠LNF=∠LEN+∠NLE=∠F,
∴LN=LF,
∴EN=LF.
∵
EN•AH=15,
∴
×5EN=15,
∴EN=6.
∴LF=6,
∴CF=3.
 解:(1)如图1,过点E作EG∥AC交BC于点G,
解:(1)如图1,过点E作EG∥AC交BC于点G,∴∠BGE=∠BCA,∠GEM=∠F,
∵∠AEF=2∠F,
∴∠GEM+∠AEF=∠F+2∠F=3∠F.
即∠AEG=3∠F.
∵AB=AC,
∴∠B=∠BCA,
∴∠BGE=∠B.
∵∠AEG=∠B+∠BGE,
∴∠AEG=2∠B,
∴3∠F=2∠B,
∴∠B=
| 3 |
| 2 |
(2)如图2,作EL∥BC交AC于L,连结NL
∴∠AEL=∠ALE=∠B=∠ACB=
| 3 |
| 2 |
∴∠LEN=2∠F-
| 3 |
| 2 |
| 1 |
| 2 |
∵EG∥AC,EL∥BC,
∴四边形EGCL是平行四边形,
∴EG=LC.
在△EGM和△FCM中,
|
∴△EGM≌△FCM(ASA),
∴EG=CF,
∴LC=CF.
∴CF=
| 1 |
| 2 |
∵∠AEL=∠ALE,
∴AE=AL.
∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD.
在△EAN和△LAN中
|
∴△EAN≌△LAN(SAS),
∴EN=LN.
∴∠LEN=∠ELN=
| 1 |
| 2 |
∵∠LNF=∠LEN+∠NLE=∠F,
∴LN=LF,
∴EN=LF.
∵
| 1 |
| 2 |
∴
| 1 |
| 2 |
∴EN=6.
∴LF=6,
∴CF=3.
点评:本题考查了等腰三角形的判定及性质的运用,全等三角形的判定及性质的运用,平行四边形的判定及性质的运用,三角形的外角与内角的关系的运用.解答时证明三角形全等是关键.

练习册系列答案
相关题目
已知a,b分别是矩形ABCD的两边,且满足a=
+
+4,若矩形的两条对角线相交所构成的锐角为α.则tanα的值为( )
| 3-b |
| b-3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
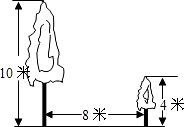 如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A、8米 | B、10米 |
| C、12米 | D、14米 |
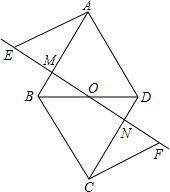 如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形.
如图,O为四边形ABCD的对角线BD的中点,过点O作一条直线分别与AB、CD交于点M、N,点E、F在直线MN上,且OE=OF,AE∥CF,AE=CF.求证:四边形ABCD是平行四边形. 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为 已知平面直角坐标系xOy(如图),直线y=
已知平面直角坐标系xOy(如图),直线y=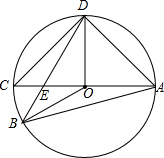 如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E. 已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;
已知二次函数C1:y=x2+2ax+2x-a+1,且a变化时,二次函数C1的图象顶点M总在抛物线C2上;