Question

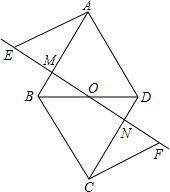如图，O为四边形ABCD的对角线BD的中点，过点O作一条直线分别与AB、CD交于点M、N，点E、F在直线MN上，且OE=OF，AE∥CF，AE=CF．求证：四边形ABCD是平行四边形．

Answer 1

考点：平行四边形的判定,全等三角形的判定与性质

专题：证明题

分析：首先连接BE、DF、ED、BF，根据BO=DO，EO=FO可得四边形EBFD是平行四边形，进而得到EB∥DF，EB=DF，DE=EF，DE∥BF，再证明△AEB≌△CFD可得AB=CD，再证明△AED≌△CFB可得AD=BC，然后根据两组对边分别相等的四边形是平行四边形得到结论．

解答：证明：连接BE、DF、ED、BF，
∵BO=DO，EO=FO，
∴四边形EBFD是平行四边形，
∴EB∥DF，EB=DF，DE=EF，DE∥BF，
∴∠2=∠1，
∵AE∥CF，
∴∠AEF=∠CFE，
∴∠AEF+∠1=∠CFE+∠2，
即∠AEB=∠CFD，
在△AEB和△CFD中，

AE=CF ∠AEB=∠CFD EB=DF

，
∴△AEB≌△CFD（SAS），
∴AB=CD，
∵ED∥BF，
∴∠DEF=∠BFE，
∴∠AEF-∠DEF=∠CFE-∠BFE，
即∠3=∠4，
在△AED和△CFB中，

AE=CF ∠3=∠4 ED=BF

，
∴△AED≌△CFB（SAS），
∴AD=BC，
∴四边形ABCD是平行四边形．

点评：此题主要考查了平行四边形的判定，关键是掌握对角线互相平分的四边形是平行四边形，两组对边分别相等的四边形是平行四边形．