��Ŀ����
 ��֪���κ���C1��y=x2+2ax+2x-a+1����a�仯ʱ�����κ���C1��ͼ��M����������C2�ϣ�
��֪���κ���C1��y=x2+2ax+2x-a+1����a�仯ʱ�����κ���C1��ͼ��M����������C2�ϣ���1���ú���a��ʽ�ӱ�ʾ����M�����꣬�����������C2�ĺ�������ʽ��
��2����������C2��ͼ����x�ύ�ڵ�A��B��A��B����ࣩ����y�ύ�ڵ�C����E��y���Ҳ���������һ�㣬����E��ֱ��AC��ƽ���߽�x���ڵ�F��������AC=2EF���Ƿ���������ĵ�E��ʹ����A��C��E��FΪ������ı��������Σ������ڣ������E�����ꣻ�������ڣ���˵�����ɣ�
��3����P��������C2�Գ�����ʹ��ACP���ܳ�ȡ����Сֵ�ĵ㣬����P������һ����y�ƽ�е�ֱ��l����������M��N���㣬��y��ƽ��MNʱ�����ֱ��l�ĺ�������ʽ��
���㣺���κ����ۺ���
ר�⣺
��������1�������䷽����y=x2+2ax+2x-a+1��д��y=��x+a+1��2-a2-3a���������M�������ǣ�-a-1��-a2-3a������������C2�ĺ�������ʽ�����ַ���������һ���ֱ�ȡa=0��-1��1���õ���������������M1��-1��0����M2��0��2����M3��-2��-4�������ô���ϵ���������������C2�ĺ�������ʽ������������-a-1=x����a=-x-1����y=-a2-3a���������������C2�ĺ�������ʽ��
��2��������������ٵ���E��x���Ϸ�ʱ������E��EH��x���ڵ�H���ɡ�CAO�ס�EFH���������������ζ�Ӧ�߳ɱ����ó�EH=
CO=1���ⷽ��-x2+x+2=1���x��ֵ���õ�E�����ꣻ�ڵ���E��x���·�ʱ��ͬ�������E�����ꣻ
��3��Ҫʹ��ACP���ܳ���С��ֻ��AP+CP��С���ɣ�����BC���Գ�����P�㣬��Ϊ��A��B����x=
�Գƣ�������Գ������Լ�����֮���߶���̣���֪��ʱAP+CP��С�����ô���ϵ�������ֱ��BC����ʽΪy=-x+2����x=
���룬���y=
���õ�P��
��
�����������P��
��
����ֱ��lΪy=kx-
k+
����M��x1��y1����N��x2��y2������y=kx-
k+
��y=-x2+x+2����������ó�x2+��k-1��x-
��k+1��=0����x1+x2=1-k=0ʱ��y��ƽ��MN���ɴ����k=1���õ�ֱ��l��y=x+1��
��2��������������ٵ���E��x���Ϸ�ʱ������E��EH��x���ڵ�H���ɡ�CAO�ס�EFH���������������ζ�Ӧ�߳ɱ����ó�EH=
| 1 |
| 2 |
��3��Ҫʹ��ACP���ܳ���С��ֻ��AP+CP��С���ɣ�����BC���Գ�����P�㣬��Ϊ��A��B����x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
����⣺��1����y=x2+2ax+2x-a+1=x2+��2a+2��x-a+1=��x+a+1��2-a2-3a��
�ඥ��M�������ǣ�-a-1��-a2-3a����
����һ���ֱ�ȡa=0��-1��1���õ���������������M1��-1��0����M2��0��2����M3��-2��-4����
������������Ķ��κ����ı���ʽ��y=-x2+x+2��
����������M��-a-1��-a2-3a������y=-x2+x+2���������ߣ�
�����=-a2-3a���ұ�=-��-a-1��2+��-a-1��+2=-a2-3a��
�����=�ұߣ�
������aȡ��ֵ������M����������y=-x2+x+2�ϣ�
�����������ߵĺ�������ʽ��C2��y=-x2+x+2��
����������-a-1=x����a=-x-1����y=-a2-3a����y=-��-x-1��2-3��-x-1��=-x2+x+2��
 �����������ߵĺ�������ʽ��C2��y=-x2+x+2��
�����������ߵĺ�������ʽ��C2��y=-x2+x+2��
��2�������������
�ٵ���E��x���Ϸ�ʱ������E��EH��x���ڵ�H��
��AC��EF��
���CAO�ס�EFH��
��
=
=2��
��EH=
CO=
��2=1����E��������Ϊ1��
��y=1ʱ��-x2+x+2=1��
���x=
��x=
����ȥ����
��E��
��1����
�ڵ���E��x���·�ʱ��ͬ�������E��
��-1����
��������������������E��������������E��
��1���� ��
��
��-1����
��3������BC���Գ�����P�㣮
�ߵ�A��B����x=
�Գƣ�
��PB=PA��
��AP+CP=BP+CP=BC��С����ACP���ܳ�=AC+AP+CP=
+BC����
��B��2��0����C��0��2����
��ֱ��BC����ʽΪy=-x+2��
�൱x=
ʱ��y=-
+2=
��
��P��
��
����
�����P��
��
����ֱ��lΪy=kx-
k+
��
��M��x1��y1����N��x2��y2����
��y=kx-
k+
��y=-x2+x+2��
��������ã�x2+��k-1��x-
��k+1��=0��
�൱x1+x2=1-k=0ʱ��y��ƽ��MN��
���k=1��
��ֱ��l�ĺ�������ʽΪy=x+1��
�ඥ��M�������ǣ�-a-1��-a2-3a����
����һ���ֱ�ȡa=0��-1��1���õ���������������M1��-1��0����M2��0��2����M3��-2��-4����
������������Ķ��κ����ı���ʽ��y=-x2+x+2��
����������M��-a-1��-a2-3a������y=-x2+x+2���������ߣ�
�����=-a2-3a���ұ�=-��-a-1��2+��-a-1��+2=-a2-3a��
�����=�ұߣ�
������aȡ��ֵ������M����������y=-x2+x+2�ϣ�
�����������ߵĺ�������ʽ��C2��y=-x2+x+2��
����������-a-1=x����a=-x-1����y=-a2-3a����y=-��-x-1��2-3��-x-1��=-x2+x+2��
 �����������ߵĺ�������ʽ��C2��y=-x2+x+2��
�����������ߵĺ�������ʽ��C2��y=-x2+x+2����2�������������
�ٵ���E��x���Ϸ�ʱ������E��EH��x���ڵ�H��
��AC��EF��
���CAO�ס�EFH��
��
| CO |
| EH |
| AC |
| EF |
��EH=
| 1 |
| 2 |
| 1 |
| 2 |
��y=1ʱ��-x2+x+2=1��
���x=
1+
| ||
| 2 |
1-
| ||
| 2 |
��E��
1+
| ||
| 2 |
�ڵ���E��x���·�ʱ��ͬ�������E��
1+
| ||
| 2 |
��������������������E��������������E��
1+
| ||
| 2 |
 ��
��1+
| ||
| 2 |
��3������BC���Գ�����P�㣮
�ߵ�A��B����x=
| 1 |
| 2 |
��PB=PA��
��AP+CP=BP+CP=BC��С����ACP���ܳ�=AC+AP+CP=
| 10 |
��B��2��0����C��0��2����
��ֱ��BC����ʽΪy=-x+2��
�൱x=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��P��
| 1 |
| 2 |
| 3 |
| 2 |
�����P��
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
��M��x1��y1����N��x2��y2����
��y=kx-
| 1 |
| 2 |
| 3 |
| 2 |
��������ã�x2+��k-1��x-
| 1 |
| 2 |
�൱x1+x2=1-k=0ʱ��y��ƽ��MN��
���k=1��
��ֱ��l�ĺ�������ʽΪy=x+1��
�����������Ƕ��κ������ۺ����ͣ������漰����֪ʶ���������ߵĶ������������ô���ϵ��������κ�����һ�κ����Ľ���ʽ�����������ε��ж������ʣ���ԳƵ����ʣ��ۺ��Խ�ǿ����һ���Ѷȣ��������ν�ϡ��������ۼ�����˼���ǽ���Ĺؼ���

��ϰ��ϵ�д�
 ��У��������ĩ��̾�ϵ�д�
��У��������ĩ��̾�ϵ�д�
�����Ŀ
����ѷ�ʽ
�е�a��b������2������÷�ʽ��ֵ��������
| a+b |
| a |
| A������2�� | B����С2�� |
| C������ | D������3�� |

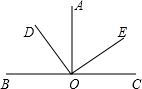 ��֪����ͼ��AO��BC��DO��OE��
��֪����ͼ��AO��BC��DO��OE�� ��֪����ͼ����Rt��ACB�У���C=90�㣬AC=4cm��BC=3cm����P��B������BA�������A�����˶�����Q��A������AC�������C�����˶�������PQ������BP=x cm��AQ=2x cm��0��x��2��������������⣺
��֪����ͼ����Rt��ACB�У���C=90�㣬AC=4cm��BC=3cm����P��B������BA�������A�����˶�����Q��A������AC�������C�����˶�������PQ������BP=x cm��AQ=2x cm��0��x��2��������������⣺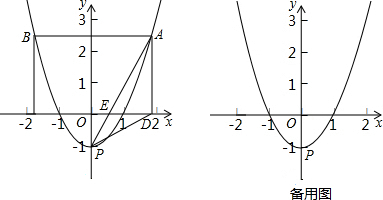
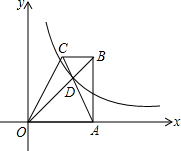 ��ֱ֪������ABCO�ĵױ�AO��x���ϣ�BC��AO��AB��AO���Խ���AC��BO�ཻ�ڵ�D��˫����y=
��ֱ֪������ABCO�ĵױ�AO��x���ϣ�BC��AO��AB��AO���Խ���AC��BO�ཻ�ڵ�D��˫����y=