题目内容
6. 如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )
如图,扇形AOB是圆锥的侧面展开图,已知圆锥的底面半径为2,母线长为6,则阴影部分的面积为( )| A. | 12π-$\frac{9\sqrt{3}}{2}$ | B. | 4π-$\frac{9\sqrt{3}}{2}$ | C. | 12π-9$\sqrt{3}$ | D. | 4π-9$\sqrt{3}$ |
分析 首先求得展开扇形的圆心角的度数,从而求得圆心到线AB的长,用扇形的面积减去三角形的面积即可求得阴影部分的面积.
解答 解:由题意知:弧长=圆锥底面周长=2×2π=4πcm,
扇形的圆心角=弧长×180÷母线长÷π=4π×180÷6π=120°.
作OC⊥AB于点C,
∴OC=$\frac{1}{2}$OA=3,AB=2AC=2×3$\sqrt{3}$=6$\sqrt{3}$,
∴S阴影=S扇形-S△AOB=$\frac{120π×{6}^{2}}{360}$-$\frac{1}{2}$×3×6$\sqrt{3}$=12π-9$\sqrt{3}$,
故选C.
点评 本题考查了圆锥的计算,用到的知识点为:弧长=圆锥底面周长及弧长与圆心角的关系,掌握公式是解答此类题目的关键,难度不大.

练习册系列答案
相关题目
11.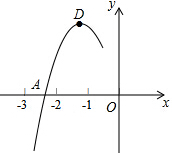 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )
 抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )
抛物线y=ax2+bx+c的顶点为D(-1,2),与x轴的一个交点A在点(-3,0)和(-2,0)之间,其部分图象如图,则以下结论不正确的是( )| A. | b2-4ac<0 | |
| B. | a+b+c<0 | |
| C. | c-a=2 | |
| D. | 方程ax2+bx+c-2=0有两个相等的实数根 |
15.下列计算正确的是( )
| A. | 4a+5b=9ab | B. | (a3)5=a15 | C. | a4•a2=a8 | D. | a6÷a3=a2 |
 一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k)x≥b-1的解集在数轴上表示正确的是( )
一次函数y=-3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式(3+k)x≥b-1的解集在数轴上表示正确的是( )







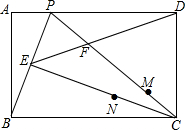 如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.
如图,在矩形ABCD中,P为AD上一点,连接BP,CP,过C作CE⊥BP于点E,连接ED交PC于点F.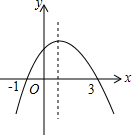 如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法:
如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法: