题目内容
11.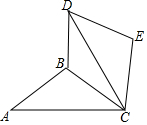 如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.
如图,△ABC中,AB=BC=5,AC=8,将△ABC绕点C顺时针方向旋转60°得到△DEC,连接BD,则BD的长度为4$\sqrt{3}$-3.
分析 如图连接AD、延长DB交AC于H.只要证明DH⊥AC,求出DH,BH即可解决问题.
解答 解:如图连接AD、延长DB交AC于H.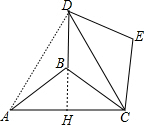
∵将△ABC绕点C顺时针方向旋转60°得到△DEC,
∴AC=DC,∠ACD=60°,
∴△ADC是等边三角形,
∴AD=DC,
在△DBA和△DBC中,
$\left\{\begin{array}{l}{DA=DC}\\{DB=DB}\\{AB=CB}\end{array}\right.$,
∴△DBA≌△DBC,
∴∠ADB=∠CDB,∵DA=DC,
∴DH⊥AC,AH=CH=4,
易知DH=$\frac{\sqrt{3}}{2}$×8=4$\sqrt{3}$,BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴DB=DH=BH=4$\sqrt{3}$-3,
故答案为4$\sqrt{3}$-3.
点评 本题考查旋转变换、等腰三角形的性质.等边三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )
| A. | 2cm | B. | 4cm | C. | 6cm | D. | 8cm |
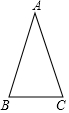 如图,△ABC中,AB=AC,∠A=36°,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C恰好仍在AC边上,∠CBD的度数是18°.
如图,△ABC中,AB=AC,∠A=36°,D为AC边上一点,将△CBD沿直线BD翻折,使翻折后的点C恰好仍在AC边上,∠CBD的度数是18°.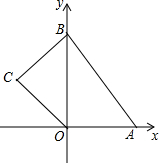 如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.
如图,在平面直角坐标系中,四边形OABC的顶点O是坐标原点,点A的坐标为(6,0),点B的坐标为(0,8),点C的坐标为(-2$\sqrt{5}$,4),点M,N分别为四边形OABC边上的动点,动点M从点O开始,以每秒1个单位长度的速度沿O→A→B路线向中点B匀速运动,动点N从O点开始,以每秒两个单位长度的速度沿O→C→B→A路线向终点A匀速运动,点M,N同时从O点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间t秒(t>0),△OMN的面积为S.