题目内容
9. 如图,△ABC内接于⊙O,AB=AC=8cm,点E,F分别在$\widehat{AB}$,$\widehat{BC}$上,∠ABC=60°.
如图,△ABC内接于⊙O,AB=AC=8cm,点E,F分别在$\widehat{AB}$,$\widehat{BC}$上,∠ABC=60°.(1)分别求出∠BDC和∠BEC的度数;
(2)若OF⊥BC于点F,求OF及OD的长度.
分析 (1)由已知条件得到△ABC是等边三角形,根据等边三角形的小猪猪即可得到结论;
(2)连接OA、OB,根据△ABC是等边三角形 且 OF⊥BC,得到A、O、F三点共线 即AF⊥BC,得到∠BAF=30°,解直角三角形得到BF=4cm,AF=4$\sqrt{3}$(cm),根据勾股定理列方程即可得到结论.
解答 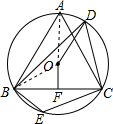 解:(1)∵AB=AC,∠ABC=60°,
解:(1)∵AB=AC,∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=BC=8cm,
∠ABC=∠ACB=∠BAC=60°,
∴∠BDC=∠BAC=60°,
∴∠BEC=120°;
(2)连接OA、OB,
∵△ABC是等边三角形 且 OF⊥BC,
∴A、O、F三点共线 即AF⊥BC,
又∵△ABC内接于⊙O,
∴OD=OA=OB,
∴在Rt△ABF中,∠BAF=30°,
∴BF=4cm,AF=4$\sqrt{3}$(cm),
设OF=x 则OB=OA=4$\sqrt{3}$-x,
在Rt△OBF中,根据勾股定理,知
OF2+BF2=OB2,
即x2+42=(4$\sqrt{3}$-x)2,
解这个方程,得 x=$\frac{4\sqrt{3}}{3}$,
∴OF=$\frac{4\sqrt{3}}{3}$ (cm),OB=4$\sqrt{3}$-$\frac{4\sqrt{3}}{3}$=$\frac{8\sqrt{3}}{3}$ (cm),OD=$\frac{8\sqrt{3}}{3}$ (cm).
点评 本题考查了三角形的外接圆与外心,等腰三角形的性质,垂径定理,勾股定理,熟练掌握各定理是解题的关键.

练习册系列答案
相关题目
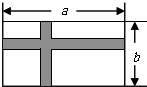 如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化.
如图,有一块长为a米、宽为b米的长方形空地,现计划在这块空地中间修出两条互相垂直的宽均为2米的道路(图中阴影部分),其余部分进行绿化. 如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°.
如图,E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,CE=$\frac{1}{4}$BC,F为CD的中点,连接AF,AE,求证:∠AFE=90°. 如图,矩形ABCD中,AB=4,BC=6,对角线AC,BD交于点O,延长DC到E,连接OE,交BC于点F.若CE=2,试求CF的长.
如图,矩形ABCD中,AB=4,BC=6,对角线AC,BD交于点O,延长DC到E,连接OE,交BC于点F.若CE=2,试求CF的长.