Question

17．如图，E，F分别是正方形ABCD中BC和CD边上的点，且AB=4，CE=$\frac{1}{4}$BC，F为CD的中点，连接AF，AE，求证：∠AFE=90°．

Answer 1

分析 先依据正方形的性质可知AD=AB=BC=CD=4，接下来求得EC、DF的长，于是可得到$\frac{DF}{AD}=\frac{EC}{CF}=\frac{1}{2}$，依据两边对应成比例且夹角相等的两个三角形相似可证明△FEC∽△AFD，由相似三角形的性质可知∠EFC=∠FAD，最后证明∠DFA+∠EFC=90°，从而可得到∠AFE=90°．

解答 证明：如图所示：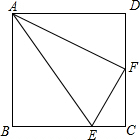

∵ABCD为正方形，
∴AB=BC=CD=AD=4．
∵CE=$\frac{1}{4}$BC，
∴CE=1．
∵F是DC的中点，
∴DF=2．
∴$\frac{DF}{AD}=\frac{EC}{CF}=\frac{1}{2}$．
又∵∠C=∠D，
∴△FEC∽△AFD．
∴∠EFC=∠FAD．
∵∠FAD+∠DFA=90°，
∴∠DFA+∠EFC=90°．
∴∠AFE=90°．

点评 本题主要考查的是相似三角形的性质和判定、正方形的性质，证得∠EFC=∠FAD是解题的关键．