Question

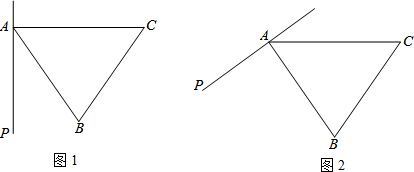
11．在等边△ABC外侧作直线AP，点B关于直线AP的对称点为D，连接BD，CD，其中CD交直线AP于点E．
（1）依题意补全图1；
（2）若∠PAB=30°，求∠ACE的度数；
（3）如图2，若60°＜∠PAB＜120°，判断由线段AB，CE，ED可以构成一个含有多少度角的三角形，并证明．

Answer 1

分析 （1）根据题意作出图形；
（2）根据题意可得∠DAP=∠BAP=30°，然后根据AB=AC，∠BAC=60°，得出AD=AC，∠DAC=120°，最后根据三角形的内角和公式求解；
（3）由线段AB，CE，ED可以构成一个含有60度角的三角形，连接AD，EB，根据对称可得∠EDA=∠EBA，然后证得AD=AC，最后即可得出∠BAC=∠BEC=60°．

解答 解：（1）所作图形如图1所示：

（2）连接AD，如图1．
∵点D与点B关于直线AP对称，
∴AD=AB，∠DAP=∠BAP=30°，
∵AB=AC，∠BAC=60°，
∴AD=AC，∠DAC=120°，
∴2∠ACE+60°+60°=180°，
∴∠ACE=30°；

（3）线段AB，CE，ED可以构成一个含有60°角的三角形．
证明：连接AD，EB，如图2．
∵点D与点B关于直线AP对称，
∴AD=AB，DE=BE，
∴∠EDA=∠EBA，
∵AB=AC，AB=AD，
∴AD=AC，
∴∠ADE=∠ACE，
∴∠ABE=∠ACE．
设AC，BE交于点F，
又∵∠AFB=∠CFE，
∴∠BAC=∠BEC=60°，
∴线段AB，CE，ED可以构成一个含有60°角的三角形．

点评 本题考查了根据轴对称变换作图以及等腰三角形的性质，解答本题的关键是根据轴对称的性质作出对应点的位置以及掌握等腰三角形的性质．