Question

16．若等腰梯形的两条对角线互相垂直，中位线长为$\sqrt{2}$，则该等腰梯形的面积是2．

Answer 1

分析 首先根据梯形中位线定理得出两底和=2$\sqrt{2}$，再由两条对角线互相垂直，得出对角线和两个底边组成等腰直角三角形，所以可求出梯形的高，进而求出梯形的面积．

解答 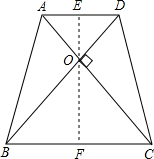解：如图，作EF⊥AD交AD，BC于E，F．
∵四边形ABCD是梯形，中位线长为$\sqrt{2}$，
∴AD+BC=2$\sqrt{2}$．
∵四边形ABCD是等腰梯形，AC⊥BD，
∴OE=$\frac{1}{2}$AD，OF=$\frac{1}{2}$BC，
∴EF=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$，
∴梯形的面积为：$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2．
故答案为2．

点评 本题考查了梯形中位线定理：梯形的中位线平行于两底，并且等于两底和的一半．也考查了等腰梯形的性质，关键知道等腰两对角线互相垂直时，对角线和底边组成的是等腰直角三角形．