题目内容
5．已知从某个多边形的一个顶点出发一共画出4条对角线，那么这个多边形共有14条对角线．分析 根据对角线的概念，知一个多边形从一个顶点出发有（n-3）条对角线，求出n的值，再根据多边形对角线的总数为$\frac{1}{2}$n（n-3），即可解答．
解答 解：∵从某个多边形的一个顶点出发一共画出4条对角线，
∴n-3=4，
∴n=7，
那么这个多边形对角线的总条数为：$\frac{1}{2}$×7×（7-3）=14．
故答案为：14．
点评 本题考查了多边形的对角线，解决本题的关键是熟记对角线的有关概念．
练习册系列答案
名校课堂系列答案
相关题目
4．
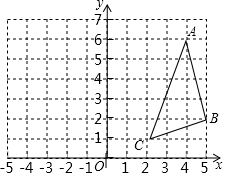如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A、B的对应点A′、B′的坐标分别是（ ）
如图，△ABC的顶点坐标分别为A（4，6）、B（5，2）、C（2，1），如果将△ABC绕点C按逆时针方向旋转90°，得到△A′B′C，那么点A、B的对应点A′、B′的坐标分别是（ ）| A． | （-3，3）、（-2，4） | B． | （3，-3）、（1，4） | C． | （3，-3）、（-2，4） | D． | （-3，3）、（1，4） |
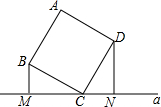如图，正方形ABCD的顶点C在直线a上，且点B，D到a的距离分别是1，2．则这个正方形的面积是5．