题目内容
等腰三角形周长为36cm,两边长之比为4:1,则底边长为( )
A. 16cm B. 4cm C. 20cm D. 16cm或4cm
 B
【解析】因为两边长之比为4:1,所以设较短一边为x,则另一边为4x;
(1)假设x为底边,4x为腰;则8x+x=36,x=4,即底边为4;
(2)假设x为腰,4x为底边,则2x+4x=36,x=6,4x=24;
∵6+6<24,∴该假设不成立.
所以等腰三角形的底边为4cm.
故选B.
B
【解析】因为两边长之比为4:1,所以设较短一边为x,则另一边为4x;
(1)假设x为底边,4x为腰;则8x+x=36,x=4,即底边为4;
(2)假设x为腰,4x为底边,则2x+4x=36,x=6,4x=24;
∵6+6<24,∴该假设不成立.
所以等腰三角形的底边为4cm.
故选B.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
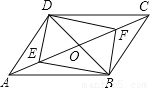
A.OE=OF B.DE=BF C.∠ADE=∠CBF D.∠ABE=∠CDF
 B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B.
B.
【解析】
试题分析:A、∵四边形ABCD是平行四边形,∴OD=OB,又∵OE=OF,∴四边形DEBF是平行四边形.能判定是平行四边形.B、DE=BF,OD=OB,缺少夹角相等.不能利用全等判断出OE=OF,∴DE=BF,∴四边形DEBF不一定是平行四边形.C、D均能证明四边形DEBF是平行四边形.
故选:B. (2016内蒙古包头市)化简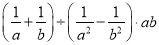 ,其结果是( )
,其结果是( )
A. 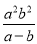 B.
B. 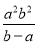 C.
C. 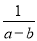 D.
D. 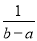
 B
【解析】= .
所以选B.
B
【解析】= .
所以选B. 化简 的结果是( )
的结果是( )
A.m+n B.n﹣m C.m﹣n D.﹣m﹣n
 A.
【解析】
试题分析:====m+n.故选A.
A.
【解析】
试题分析:====m+n.故选A. △ABC中,若∠A=80°,∠B=50°,AC=5,则AB= .
 5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5.
5.
【解析】
试题解析:∵∠A=80°,∠B=50°,
∴∠C=180°-80°-50°=50°,
∴AB=AC=5. 在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )

A. 4 cm B. 2 cm C. 3 cm D. 1 cm
 C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
故选C.
C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
故选C. 等腰△ABC中,AB=AC,一边上的中线BD将这个三角形的周长分为15和12两个部分,则这个等腰三角形的底边长为( )
A. 7 B. 11 C. 7或11 D. 7或10
 C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
...
C
【解析】试题分析:题中给出了周长关系,要求底边长,首先应先想到等腰三角形的两腰相等,寻找问题中的等量关系,列方程求解,然后结合三角形三边关系验证答案.设等腰三角形的底边长为x,腰长为y,则根据题意,得①或②,解方程组①得:x=11,y=8,根据三角形三边关系定理,此时能组成三角形;解方程组②得:x=7,y=10,根据三角形三边关系定理此时能组成三角形,即等腰三角形的底边长是11或7.
... 三角形中∠B的平分线和外角的平分线的夹角是( ).
A. 60° B. 90° C. 45° D. 135°
 B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B.
B
【解析】
如图,BD平分∠ABF,BE平分∠ABC,
∴∠ABD=∠ABF,∠ABE=∠ABC,
∴∠DBE=∠DBA+∠ABE=∠ABF+∠ABC=(∠ABF+∠ABC)=90°.
故选B. (x+5y)2 等于( )
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C.
C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C. 
