题目内容
13.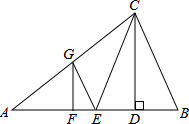 如图,在△ABC中,CD是高,CE是中线,CE=CB,AF=DF,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.
如图,在△ABC中,CD是高,CE是中线,CE=CB,AF=DF,过点F作FG∥CD,交AC边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为27.
分析 先根据点A、D关于点F对称可知点F是AD的中点,再由CD⊥AB,FG∥CD可知FG是△ACD的中位线,故可得出CG的长,再根据点E是AB的中点可知GE是△ABC的中位线,故可得出GE的长,由此可得出结论.
解答 解:∵点A、D关于点F对称,
∴点F是AD的中点.
∵CD⊥AB,FG∥CD,
∴FG是△ACD的中位线,AC=18,BC=12,
∴CG=$\frac{1}{2}$AC=9.
∵点E是AB的中点,
∴GE是△ABC的中位线,
∵CE=CB=12,
∴GE=$\frac{1}{2}$BC=6,
∴△CEG的周长=CG+GE+CE=9+6+12=27.
故答案为:27.
点评 本题考查的是三角形中位线定理,熟知三角形的中位线平行于第三边,并且等于第三边的一半是解答此题的关键.

练习册系列答案
相关题目
18.在一次野炊活动中,小明所在的班级有x人,分成y组,若每组7人,则余下3人;若每组8人,则缺5人,求全班人数的正确的方程组是( )
| A. | $\left\{\begin{array}{l}{7y=x-3}\\{8y=x+5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{7y=x+3}\\{8y=x-5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{7x=y+3}\\{8x=y-5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{7x=y-3}\\{8x=y+5}\end{array}\right.$ |
5.用反证法证明命题:若整数系数一元二次方程ax2+bx+c=0(a≠0)有有理根,那么a、b、c中至少有一个是偶数时,下列假设中正确的是( )
| A. | 假设a、b、c都是偶数 | B. | 假设a、b、c至多有一个是偶数 | ||
| C. | 假设a、b、c都不是偶数 | D. | 假设a、b、c至多有两个是偶数 |
 某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动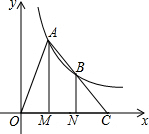 如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.
如图,点A,B在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,过点A,B作x轴的垂线,垂足分别为M,N,延长线段AB交x轴于点C,若OM=MN=NC,且△BNC的面积为4,则k值为16.