Question

10．正方形ABCD的边长为4，点E为直线BC上一点，且CE=2，连接AE，作EF⊥AE交射线DC于F，求CF的长为1或3．

Answer 1

分析 首先根据题意画出图形，分别从当点E在线段BC上与点E在BC的延长线上去分析求解即可求得答案．

解答 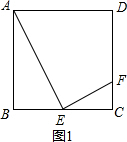解：如图1，当点E在线段BC上时，
∵四边形ABCD是正方形，
∴∠B=∠C=90°，AB=BC=4，
∴∠BAE+∠AEB=90°，
∵CE=2，
∴BE=BC-CE=2，
∵EF⊥AE，
∴∠AEB+∠CEF=90°，
∴∠BAE=∠CEF，
∴△ABE∽△ECF，
∴AB：EC=BE：CF，
∴4：2=2：CF，
解得：CF=1；
如图2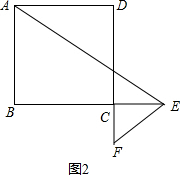，若点E在BC的延长线上时，
∵四边形ABCD是正方形，
∴∠B=∠BCD=∠ECF=90°，
∵EF⊥AE，
∴∠AEB+∠CEF=90°，∠CEF+∠F=90°，
∴∠AEB=∠F，
∴△ABE∽△ECF，
∴AB：EC=BE：CF，
∴4：2=6：CF，
解得：CF=3．
综上所述，CF=1或3．
故答案为：1或3．

点评 此题考查了相似三角形的判定与性质以及正方形的性质．注意掌握分类讨论思想的应用是解此题的关键．