题目内容
13.关于$\sqrt{12}$的叙述,错误的是( )| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$是12的算术平方根 | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
分析 根据无理数的定义、算术平方根及数轴的知识进行判断.
解答 解:A、$\sqrt{12}$是无理数,所以此选项说法错误;
B、面积为12的正方形边长是$\sqrt{12}$,所以此选项说法正确;
C、$\sqrt{12}$是12的算术平方根,所以此选项说法正确;
D、因为数轴上的点对应任意实数,所以在数轴上可以找到表示$\sqrt{12}$的点,所以此选项说法正确;
本题选择错误的选项,故选A.
点评 此题主要考查了无理数的定义和数轴的知识,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
1.如图,∠1和∠2是对顶角的是( )
| A. |  | B. |  | C. |  | D. |  |
5.下列各式中正确的是( )
| A. | $\root{3}{64}$=4 | B. | $\sqrt{16}$=±4 | C. | $\sqrt{-9}$=3 | D. | $\sqrt{2\frac{1}{4}}$=$\frac{3}{4}$ |
 如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.
如图,若四边形ABCD是平行四边形,E、F分别是AB,AD边上的点,DE与CF交于点G,若E为AB的中点,AF=2FD,求$\frac{DG}{EG}+\frac{CG}{FG}$的值.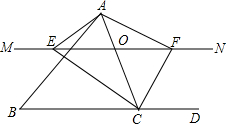 已知在△ABC中,D为边BC延长线上一点,点O是边AC上的一个动点,过O做直线MN∥BC,设MN与∠BCA的平分线相交于点E,与∠ACD的平分线相交于点F.
已知在△ABC中,D为边BC延长线上一点,点O是边AC上的一个动点,过O做直线MN∥BC,设MN与∠BCA的平分线相交于点E,与∠ACD的平分线相交于点F.