题目内容
3.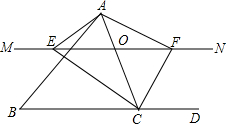 已知在△ABC中,D为边BC延长线上一点,点O是边AC上的一个动点,过O做直线MN∥BC,设MN与∠BCA的平分线相交于点E,与∠ACD的平分线相交于点F.
已知在△ABC中,D为边BC延长线上一点,点O是边AC上的一个动点,过O做直线MN∥BC,设MN与∠BCA的平分线相交于点E,与∠ACD的平分线相交于点F.(1)求证:OE=OF;
(2)试确定点O在边AC上的位置,使四边形AECF是矩形,并加以证明.
(3)在(2)的条件下,且△ABC满足∠ACB=90°条件时,矩形AECF是正方形?.
分析 (1)角平分线到角两边的距离相等,再利用全等三角形即可求解.
(2)探究性问题,归根究底还是对矩形性质的判定,再平行四边形的基础上,加上其对角线平分且相等即可.
(3)正方形的判定,在(2)的基础上,即在矩形的基础上补充对角线垂直即可.
解答 解:(1)如图所示:作EG⊥BC,EJ⊥AC,FK⊥AC,FH⊥BC,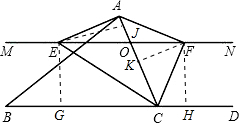
因为直线EC,CF分别平分∠ACB与∠ACD,所以EG=EJ,FK=FH,
在△EJO与△FKO中,
$\left\{\begin{array}{l}{∠AOE=∠CON}\\{∠EJO=∠FKO}\\{EJ=FK}\end{array}\right.$,
所以△EJO≌△FKO,即OE=OF;
(2)当OA=OC,OE=OF时,四边形AECF是矩形,
证明:∵OA=OC,OE=OF,
∴四边形AECF为平行四边形,
又∵直线MN与∠BCA的平分线相交于点E,与∠DCA(△ABC的外角)的平分线相交于点F.
∴∠ACE=∠BCE,∠ACF=∠FCD,
由∠BCE+∠ACE+∠ACF+∠FCD=180°,
∴∠ECA+∠ACF=90°,即∠ECF=90°,
∴四边形AECF为矩形;
(3)由(2)可知,四边形AECF是矩形,要使其为正方形,再加上对角线垂直即可,即∠ACB=90°.
故答案为:∠ACB=90°
点评 此题考查正方形的判定问题,掌握角平分线到角两边距离相等,以及正方形,矩形的性质及判定定理.

练习册系列答案
相关题目
13.关于$\sqrt{12}$的叙述,错误的是( )
| A. | $\sqrt{12}$是有理数 | B. | 面积为12的正方形边长是$\sqrt{12}$ | ||
| C. | $\sqrt{12}$是12的算术平方根 | D. | 在数轴上可以找到表示$\sqrt{12}$的点 |
18.小明统计了他家今年3月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过10min的频率为( )
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 20 | 15 | 9 | 6 |
| A. | 0.1 | B. | 0.3 | C. | 0.5 | D. | 0.7 |
15.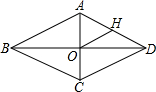 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
 如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )| A. | 6cm | B. | 4cm | C. | 3cm | D. | 2cm |
 如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.
如图所示,已知AB∥DC,AE平分∠BAD,CD与AE相交于点F,∠CFE=∠E,试说明AD∥BC.