题目内容
10．
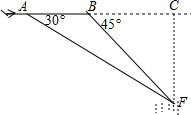“马航事件”的发生引起了我国政府的高度重视，我国政府迅速派出了舰船和飞机到相关海域进行搜寻．如图，在一次空中搜寻中，水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体（该物体视为静止）．此时的俯角为30°，为了便于观察，飞机继续向前飞行了800米到达B点，此时测得点F点俯角为45°．请你计算当飞机飞临F点的正上方点C时（点A、B、C在同一直线上），竖直高度CF约为多少米？（结果保留整数，参考数值：$\sqrt{3}$≈1.7）
分析 设CF=x，根据正切的概念列出方程，解方程即可．
解答 解：设CF=x，
∵∠BCF=90°，∠FBC=45°，
∴BC=CF=x，
在Rt△ACF中，tanA=$\frac{CF}{AC}$，
∴$\frac{x}{x+800}$=$\frac{\sqrt{3}}{3}$，
解得，x=400$\sqrt{3}$+400，
∴CF=400$\sqrt{3}$+400≈1080（米），
答：竖直高度CF约为1080米．
点评 本题考查的是解直角三角形的应用，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．
练习册系列答案
相关题目
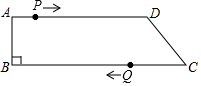如图，在四边形ABCD中，AD∥BC，∠B=90°，AB=8cm，AD=24cm，BC=30cm．点P从点A出发，以1cm/s的速度向点D移动，点Q从点C出发，以3cm/s的速度向点B运动，点P和点Q分别从点A和点C同时出发，移动时间为ts．规定若其中一个动点先到达端点（终点）时，另一个动点也随之停止运动．
2．某工厂甲、乙两名工人参加操作技能培训，现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次，记录如下：
（1）请你分别计算这两组数据的平均数；
（2）现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．
| 甲 | 85 | 88 | 84 | 85 | 83 |
| 乙 | 83 | 87 | 84 | 86 | 85 |
（2）现要从中选派一人参加操作技能比赛，从统计学的角度考虑，你认为选派哪名工人参加合适？请说明理由．
已知抛物线y=ax2+x+c（a≠0）经过点A（-1，0），B（2，0）两点，与y轴相交于点C，点D为抛物线的顶点．