题目内容
2.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:| 甲 | 85 | 88 | 84 | 85 | 83 |
| 乙 | 83 | 87 | 84 | 86 | 85 |
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
分析 (1)根据平均数的概念列式计算即可得解;
(2)求出两人测试成绩的方差,然后根据方差越小越稳定选择合适人选.
解答 解:(1)甲平均数:$\frac{1}{5}$×(85+88+84+85+83)=$\frac{1}{5}$×425=85,
乙平均数:$\frac{1}{5}$×(83+87+84+86+85)=$\frac{1}{5}$×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=$\frac{1}{5}$×[(85-85)2+(88-85)2+(84-85)2+(85-85)2+(83-85)2],
=$\frac{1}{5}$×(0+9+1+0+4),
=2.8,
S乙2=$\frac{1}{5}$×[(83-85)2+(87-85)2+(84-85)2+(86-85)2+(85-85)2],
=$\frac{1}{5}$×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.
点评 本题考查了算术平均数,方差,平均数表示一组数据的平均程度,方差是用来衡量一组数据波动大小的量.

练习册系列答案
相关题目
17.为了了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成下表:
(1)根据上表的数据,写出用t表示Q的关系式;
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为55L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了46L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
| 汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … |
| 油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(2)汽车行驶5h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为55L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了46L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
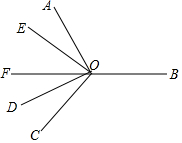 如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论:
如图,在平面内,∠AOB=∠COB,∠AOD=∠COE=90°,OF平分∠DOE,则以下结论: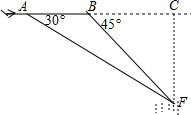 “马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,我国政府迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机在点A处测得前方海面的点F处有疑似飞机残骸的物体(该物体视为静止).此时的俯角为30°,为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F点俯角为45°.请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7) 如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.
如图,在?ABCD中,CE平分∠BCD,交AD于点E,DF平分∠ADC,交BC于点F,CE与DF交于点P,连接EF,BP.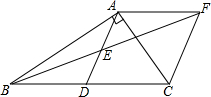 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.